Question

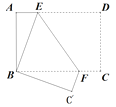
【题目】已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：

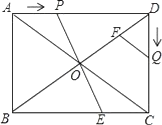
（1）当t为何值时，△AOP是等腰三角形？

（2）设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；

（3）在运动过程中，是否存在某一时刻t，使S五边形S五边形OECQF：S△ACD=9：16？若存在，求出t的值；若不存在，请说明理由；

（4）在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）或5；（2）；（3）；（4）2.88.

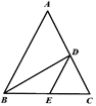
【解析】试题（1）根据矩形的性质和勾股定理得到AC=10，①当AP=PO=t，如图1，过P作PM⊥AO，根据相似三角形的性质得到AP=t=，②当AP=AO=t=5，于是得到结论；

（2）作EH⊥AC于H，QM⊥AC于M，DN⊥AC于N，交QF于G，根据全等三角形的性质得到CE=AP=t，根据相似三角形的性质表示出EH，根据相似三角形的性质表示出QM，FQ，根据图形的面积即可得到结论；

（3）根据题意列方程得到t的值，于是得到结论；

（4）由角平分线的性质得到DM的长，根据勾股定理得到ON的长，由三角形的面积公式表示出OP，根据勾股定理列方程即可得到结论．

试题解析：（1）∵在矩形ABCD中，Ab=6cm，BC=8cm，

∴AC=10，

①当AP=PO=t，如图1，过P作PM⊥AO，

∴AM=AO=，

∵∠PMA=∠ADC=90°，∠PAM=∠CAD，

∴△APM∽△ADC，

∴，

∴AP=t=，

②当AP=AO=t=5，

∴当t为或5时，△AOP是等腰三角形；

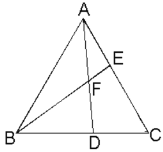
（2）作EH⊥AC于H，QM⊥AC于M，DN⊥AC于N，交QF于G，在△APO与△CEO中，

∵∠PAO=∠ECO，AO=OC，∠AOP=∠COE，

∴△AOP≌△COE，

∴CE=AP=t，

∵△CEH∽△ABC，

∴，

∴EH=，

∵DN==，

∵QM∥DN，

∴△CQM∽△CDN，

∴，即，

∴QM=，

∴DG==，

∵FQ∥AC，

∴△DFQ∽△DOC，

∴，

∴FQ=，

∴S五边形OECQF=S△OEC+S四边形OCQF==，

∴S与t的函数关系式为；

（3）存在，

∵S△ACD=×6×8=24，

∴S五边形OECQF：S△ACD=（）：24=9：16，解得t=，t=0，（不合题意，舍去），

∴t=时，S五边形S五边形OECQF：S△ACD=9：16；

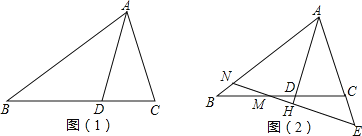
（4）如图3，过D作DM⊥AC于M，DN⊥AC于N，

∵∠POD=∠COD，

∴DM=DN=，

∴ON=OM==，

∵OPDM=3PD，

∴OP=，

∴PM=，

∵，

∴，解得：t≈15（不合题意，舍去），t≈2.88，

∴当t=2.88时，OD平分∠COP．