题目内容
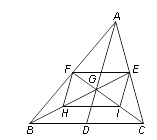
【题目】如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1)求证:四边形EFHI是平行四边形;
(2)①当AD与BC满足条件 时,四边形EFHI是矩形;
②当AD与BC满足条件 时,四边形EFHI是菱形.
【答案】(1)证明见解析;(2)①AD⊥BC;②2AD=3BC
【解析】试题分析:(1)证出EF、HI分别是△ABC、△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=![]() BC,HI∥BC且PQ=
BC,HI∥BC且PQ=![]() BC,进而可得EF∥HI且EF=HI.根据一组对边平行且相等的四边形是平行四边形可得结论;
BC,进而可得EF∥HI且EF=HI.根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)①由三角形中位线定理得出FH∥AD,再证出EF⊥FH即可;
②与三角形重心定理得出AG=![]() AD,证出AG=BC,由三角形中位线定理和添加条件得出FH=EF,即可得出结论.
AD,证出AG=BC,由三角形中位线定理和添加条件得出FH=EF,即可得出结论.
试题解析:(1)证明:∵BE,CF是△ABC的中线,∴EF是△ABC的中位线,∴EF∥BC且EF=![]() BC.
BC.
∵H、I分别是BG、CG的中点.,∴HI是△BCG的中位线,∴HI∥BC且HI=![]() BC,∴EF∥HI且EF=HI,∴四边形EFHI是平行四边形.
BC,∴EF∥HI且EF=HI,∴四边形EFHI是平行四边形.
(2)解:①当AD与BC满足条件 AD⊥BC时,四边形EFHI是矩形;理由如下:
同(1)得:FH是△ABG的中位线,∴FH∥AG,FH=![]() AG,∴FH∥AD,∵EF∥BC,AD⊥BC,∴EF⊥FH,∴∠EFH=90°,∵四边形EFHI是平行四边形,∴四边形EFHI是矩形;
AG,∴FH∥AD,∵EF∥BC,AD⊥BC,∴EF⊥FH,∴∠EFH=90°,∵四边形EFHI是平行四边形,∴四边形EFHI是矩形;
故答案为:AD⊥BC;
②当AD与BC满足条件BC=![]() AD时,四边形EFHI是菱形;理由如下:
AD时,四边形EFHI是菱形;理由如下:
∵△ABC的中线AD、BE、CF相交于点G,∴AG=![]() AD,∵BC=
AD,∵BC=![]() AD,∴AG=BC,∵FH=
AD,∴AG=BC,∵FH=![]() AG,EF=
AG,EF=![]() BC,∴FH=EF,又∵四边形EFHI是平行四边形,∴四边形EFHI是菱形;
BC,∴FH=EF,又∵四边形EFHI是平行四边形,∴四边形EFHI是菱形;
故答案为:2AD=3BC.

 阅读快车系列答案
阅读快车系列答案
