题目内容
如图①已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.
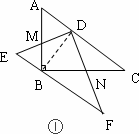
(1)在图①中,DE交AB于M,DF交BC于N,①证明:DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分DMBN,请说明四边形DMBN的面积是否发生变化,若发生变化,请说明四边形DMBN如何变化.若不变,求其面积.
(2)继续旋转至如图②延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立请给出证明;若不成立,请说明理由?

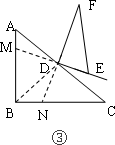
(3)继续转至图③延长FD交BC于N延长ED交AB于M,DM=DN是否仍然成立?若成立请直接写出结论,不用证明.
答案:
解析:
解析:
|
(1)①AD=BD=DC,∠MBD=∠CND=45°,∠MDB=∠NDC→△MDB≌△NDC→MD=ND ②不发生变化,SMDNB= (2)成立,证明过程同(1) (3)成立. |

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.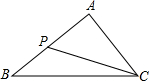 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )