题目内容
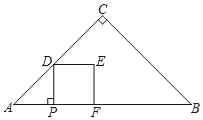
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=8.点P从点A出发,以每秒2个单位长度的速度沿边AB向点B运动.过点P作PD⊥AB交折线AC﹣CB于点D,以PD为边在PD右侧做正方形PDEF.设正方形PDEF与△ABC重叠部分图形的面积为S,点P的运动时间为t秒(0<t<4).
(1)当点D在边AC上时,正方形PDEF的边长为 (用含t的代数式表示).
(2)当点E落在边BC上时,求t的值.
(3)当点D在边AC上时,求S与t之间的函数关系式.
(4)作射线PE交边BC于点G,连结DF.当DF=4EG时,直接写出t的值.
【答案】(1)2t;(2)![]() ;(3)
;(3) ;(4)t=
;(4)t=![]() 或
或![]()
【解析】
(1)由等腰直角三角形的性质和正方形的性质可得:∠A=∠ADP=45°,即AP=DP=2t;
(2)由等腰直角三角形的性质和正方形的性质可得:AB=AP+PF+FB,即2t+2t+2t=8,可求t的值;
(3)分两种情况讨论,根据重叠部分的图形的形状,可求S与t之间的函数关系式;
(4)分点E在△ABC内部和△ABC外部两种情况讨论,根据平行线分线段成比例,可求t的值.
(1)∵∠C=90°,AC=BC,
∴∠A=45°=∠B,且DP⊥AB,
∴∠A=∠ADP=45°,
∴AP=DP=2t,
故答案为2t,
(2)如图,

∵四边形DEFP是正方形,
∴DP=DE=EF=PF,∠DPF=∠EFP=90°,
∵∠A=∠B=45°,
∴∠A=∠ADP=∠B=∠BEF=45°,
∴AP=DP=2t=EF=FB=PF,
∵AB=AP+PF+FB,
∴2t+2t+2t=8,
∴t=![]() ;
;
(3)当0<t≤![]() 时,正方形PDEF与△ABC重叠部分图形的面积为正方形PDEF的面积,
时,正方形PDEF与△ABC重叠部分图形的面积为正方形PDEF的面积,
即S=DP2=4t2,
当![]() <t≤2时,如图,正方形PDEF与△ABC重叠部分图形的面积为五边形PDGHF的面积,
<t≤2时,如图,正方形PDEF与△ABC重叠部分图形的面积为五边形PDGHF的面积,

∵AP=DP=PF=2t,
∴BF=8﹣AP﹣PF=8﹣4t,
∵BF=HF=8﹣4t,
∴EH=EF﹣HF=2t﹣(8﹣4t)=6t﹣8,
∴S=S正方形DPFE﹣S△GHE,
∴S=4t2﹣![]() ×(6t﹣8)2=﹣14t2+48t﹣32,
×(6t﹣8)2=﹣14t2+48t﹣32,
综上所述,S与t之间的函数关系式为 .
.
(4)如图,当点E在△ABC内部,设DF与PE交于点O,

∵四边形PDEF是正方形,
∴DF=PE=2PO=2EO,∠DFP=45°,
∴∠DFP=∠ABC=45°,
∴DF∥BC,
∴![]() ,
,
∵DF=4EG,
∴设EG=a,则DF=4a=PE,PO=2a=EO,
∴PG=5a,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
如图,当点E在△ABC外部,设DF与PE交于点O,

∵四边形PDEF是正方形,
∴DF=PE=2PO=2EO,∠DFP=45°,
∴∠DFP=∠ABC=45°,
∴DF∥BC,
∴![]() ,
,
∵DF=4EG,
∴设EG=a,则DF=4a=PE,PO=2a=EO,
∴PG=3a,
∵![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
综上所述:t=![]() 或
或![]() .
.