Question

【题目】在直线上摆放着三个正方形

(1)如图1，已知水平放置的两个正方形的边长依次是，斜着放置的正方形的面积_ ；两个直角三角形的面积之和为____ (均用表示)

(2)如图2，小正方形面积， 斜着放置的正方形的面积，求图中两个钝角三角形的面积_ ；_

(3)图3是由五个正方形所搭成的平面图，与分别表示所在地三角形与正方形的面积，试写出_ ；_ .(均用表示)

Answer 1

【答案】（1）=，；（2）=，=；（3）=,=.

【解析】

（1）根据题意，可先证明中间两个三角形全等，再根据勾股定理求解即可；

（2）求出两个钝角三角形的底边和高，再根据三角形面积公式求解即可；

（3）连接BC，由（1）可得S，由（2）可得T=，然后利用大的不规则图形面积减去一个图中的梯形面积即可算出的值，进而得出答案即可.

（1）如图1所示，先将各点标记于图上；

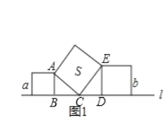
∵三个四边形均为正方形，

∴∠ACB＋∠BAC=90°，∠ACB＋∠DCE=90°，AC=CE，

∴∠BAC=∠DCE，

∵∠ABC=∠CDE=90°，

∴△ABC≌△CDE

∴BC=DE=b，AB=CD=，

△ABC面积＋△CDE面积=，

同时：=，

即=，

所以斜着放置的正方形的面积；两个直角三角形的面积之和为；

（2）如图2所示，用虚线画出m1，m2的高，

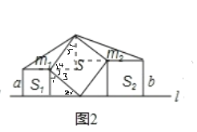
∵小正方形面积为1，∴，

又∵斜正方形面积为4，∴斜正方形边长为2，，即，

易得：∠2=30°（30°角所对应的直角边是斜边的一半），

∴∠1=60°，

∵∠3＋∠4=90°，

∴∠4＝∠1=60°，

∴∠5=30°，

又∵斜放的正方形边长为2，

∴钝角三角形m1的高为，

同理可得钝角三角形m2的高为1，

∴钝角三角形m1的面积=，

钝角三角形m2的面积=,.

（3）如图3所示，标识出各点，连接BC，

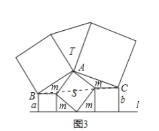
由（1）可得：=，

由（2）可得：T=

又由（1）、（2）可得：图中四个小三角形面积，

∴==

即=.