题目内容
边长为a的正n边形的外接圆与内切圆围成的圆环的面积为______．
如右图所示，
AB为正n边形的一边，正n边形的中心为O，AB与小圆切于点C，连接OA，OC，
则OC⊥AB，AC=
AB=
a，
所以在Rt△AOC中，根据勾股定理得：AC2=
a2=OA2-OC2，
则S圆环=S大圆-S小圆=πOA2-πOC2=π（OA2-OC2）=
a2．
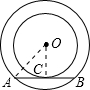
AB为正n边形的一边，正n边形的中心为O，AB与小圆切于点C，连接OA，OC，
则OC⊥AB，AC=
| 1 |
| 2 |
| 1 |
| 2 |
所以在Rt△AOC中，根据勾股定理得：AC2=
| 1 |
| 4 |
则S圆环=S大圆-S小圆=πOA2-πOC2=π（OA2-OC2）=
| π |
| 4 |
练习册系列答案
相关题目
为1厘米和2厘米．当两圆相交时，⊙O的运动时间t（秒）的取值范围是______．
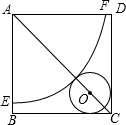
任一点（点C、D均不与A、B重合）．
