题目内容
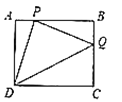
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 上的动点,且
上的动点,且![]() ,当
,当![]() 为等腰三角形时,则
为等腰三角形时,则![]() 的长为______.
的长为______.
【答案】1或7
【解析】
当P点在AB上,如图1,先根据等角的余角相等得到∠ADP=∠BPQ,则可证明Rt△ADP∽Rt△BPQ,利用相似比得到![]() =1,则PB=AD=3,然后计算AB-PB即可.当P点在AB的延长线上时,如图2,同样方法得到Rt△ADP∽Rt△BPQ,利用相似比得到PB=AD=3,然后计算AB+PB即可.
=1,则PB=AD=3,然后计算AB-PB即可.当P点在AB的延长线上时,如图2,同样方法得到Rt△ADP∽Rt△BPQ,利用相似比得到PB=AD=3,然后计算AB+PB即可.
解:当P点在边AB上,如图1,
∵四边形ABCD为矩形,
∴AD=BC=3,∠A=∠B=90°,
∵PD⊥PQ,
∴∠DPQ=90°,
∵∠APD+∠ADP=90°,∠APD+∠BPQ=90°,
∴∠ADP=∠BPQ,
∴Rt△ADP∽Rt△BPQ,
∴![]() ,
,
∴PB=AD=3,
∴AP=AB-PB=4-3=1.
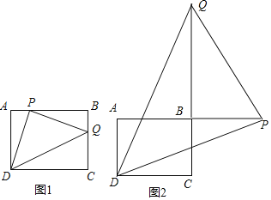
当P点在AB的延长线上时,如图2,
同样方法得到Rt△ADP∽Rt△BPQ,
∴![]() =1,
=1,
∴PB=AD=3,
∴AP=AB+PB=4+3=7.
综上所述,AP的长度为1或7.
故答案为1或7.
故答案为1或7.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目