Question

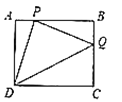
【题目】在△ABC中，∠ACB＝90°，AC＝6，BC＝8，D边BC上的任意一点，将∠C沿过点D的直线折叠，使点C落在斜边AB上的点E处，当△BDE是直角三角形时，CD的长为_____．

Answer 1

【答案】3或.

【解析】

依据沿过点D的直线折叠，使直角顶点C落在斜边AB上的点E处，当△BDE是直角三角形时，分两种情况讨论：∠DEB＝90°或∠BDE＝90°，分别依据勾股定理或者相似三角形的性质，即可得到CD的长．

分两种情况：

①若∠DEB＝90°，则∠AED＝90°＝∠C，CD＝ED，

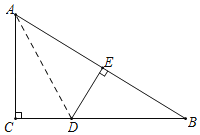
连接AD，则Rt△ACD≌Rt△AED（HL），

∴AE＝AC＝6，BE＝10﹣6＝4，

设CD＝DE＝x，则BD＝8﹣x，

∵Rt△BDE中，DE2+BE2＝BD2，

∴x2+42＝（8﹣x）2，

解得x＝3，

∴CD＝3；

②若∠BDE＝90°，则∠CDE＝∠DEF＝∠C＝90°，CD＝DE，

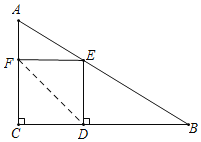
∴四边形CDEF是正方形，

∴∠AFE＝∠EDB＝90°，∠AEF＝∠B，

∴△AEF∽△EBD，

∴＝，

设CD＝x，则EF＝CF＝x，AF＝6﹣x，BD＝8﹣x，

∴＝，

解得x＝，

∴CD＝，

综上所述，CD的长为3或.