题目内容
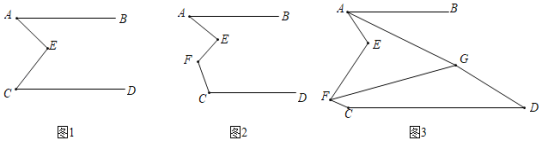
【题目】如图,AB∥CD.
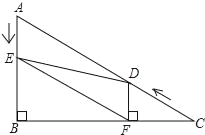
(1)如图1,∠A、∠E、∠C的数量关系为 .
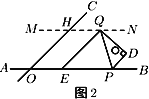
(2)如图2,若∠A=50°,∠F=115°,求∠C﹣∠E的度数;
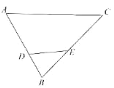
(3)如图3,∠E=90°,AG,FG分别平分∠BAE,∠CFE,若GD∥FC,试探究∠AGF与∠GDC的数量关系,并说明理由.
【答案】(1)∠AEC=∠C+∠A;(2)∠C﹣∠E=15°;(3)2∠AGF+∠GDC=90°.理由见解析.
【解析】
(1)过点E作EF∥AB,知AB∥CD∥EF,据此得∠A=∠AEF,∠C=∠CEF,根据∠AEC=∠AEF+∠CEF可得答案;
(2)分别过点E、F作FM∥AB,EN∥AB,设∠NEF=x=∠EFM,知∠AEF=x+50°,∠MFC=115°-x,据此得∠C=180°-(115°-x)=x+65°,进一步计算可得答案;
(3)分别过点E、F、G作FM∥AB,EN∥AB,GH∥AB,设∠GAE=x=∠GAB,∠GFM=y,∠MPC=z,知∠GPE=y+z,从而得2x+2y+z=90°,∠C=180°-z,根据GD∥FC得∠D=z,由GH∥AB,AB∥CD知∠AGF=x+y,继而代入可得答案.
(1)∠AEC=∠C+∠A,
如图1,过点E作EF∥AB,
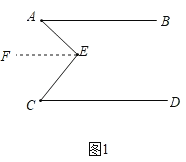
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A=∠AEF,∠C=∠CEF,
则∠AEC=∠AEF+∠CEF=∠A+∠C,
故答案为:∠AEC=∠C+∠A;
(2)如图2,分别过点E、F作FM∥AB,EN∥AB,
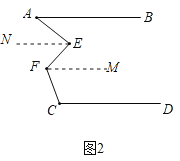
设∠NEF=x=∠EFM,则∠AEF=x+50°,∠MFC=115°﹣x,
∴∠C=180°﹣(115°﹣x)=x+65°,
∴∠C﹣∠E=x+65°﹣(x+50°)=15°;
(3)如图3,分别过点E、F、G作FM∥AB,EN∥AB,GH∥AB,
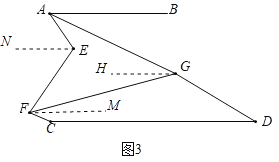
设∠GAE=x=∠GAB,∠GFM=y,∠MPC=z,
则∠GPE=y+z,
∴2x+2y+z=90°,∠C=180°﹣z,
∵GD∥FC,
∴∠D=z,
∵GH∥AB,AB∥CD,
∴∠AGF=x+y,
∴2∠AGF+∠GDC=90°.

 阅读快车系列答案
阅读快车系列答案【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
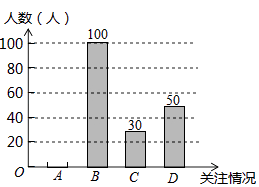
(1)根据上述统计表可得此次采访的人数为人;m= , n=;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约人.