题目内容
【题目】如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(一6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.

(1)直接写出线段BO的长:
(2)求点D的坐标;
(3)若点N是平面内任一点,在x轴上是否存在点M,使咀M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标:若不存在,请说明理由.
【答案】(1)BO=10;(2)D(0,5);(3)存在,, M(4,0),(-4,0)(![]() ,0)(
,0)(![]() ,0).
,0).
【解析】
(1)由矩形的性质及勾股定理即可求出BO的长;(2)由折叠的性质可得BE=AB=6,DE=AD,故OE=BO-BE=4,∠OED=90°,设D(0,a)则OD=a,DE=AD=OA-OD=8-a,在Rt△EOD中,由勾股定理得到方程即可求出a的值;(3)分①OM,OE都为边;②OM为边OE为对角线;③OM为对角线,OE为边;3种情况进行讨论,分别求出M的坐标.
解:(1)∵四边形ABCO是矩形,点B坐标为(-6,8)
∴BO=![]() =10
=10
(2)∵矩形ABCO中点B的坐标是(-6,8)
∴AB=6,OA=8.
BE=AB=6,OE=10-6=4
设D(0,a),则OD=a,AD=ED=8-a
在RtΔEOD中,![]()
![]()
解得:a=5.
∴D(0,5)
(3)存在,
①OM,OE都为边时,OM=OE=4,
∴M的坐标为(4,0),(-4,0)
②OM为边OE为对角线时,MN垂直平分OE,垂足为G,如图1
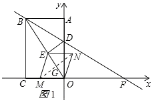
则OG=![]() OE=2
OE=2
则cos∠MOG=cos∠BOC
∴![]() 即
即![]()
解得OM=![]()
∴M(![]() ,0)
,0)
③OM为对角线,OE为边,如图2
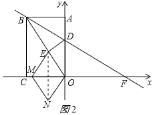
同②得M(![]() ,0)
,0)
∴M(4,0),(-4,0)(![]() ,0)(
,0)(![]() ,0).
,0).

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】某地台风带来严重灾害,该市组织20辆汽车装食品、药品、生活用品三种救灾物质共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同种物质且必须装满.根据表格提供的信息,解答下列问题:
物资种类 | 食品 | 药品 | 生活用品 |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨所需运费(元/吨) | 120 | 160 | 100 |
(1)若装食品的车辆是5辆,装药品的车辆为__________辆;
(2)设装食品的车辆为x辆,装药品的车辆为y辆,求y与x的函数关系式;
(3)如果装食品的车辆不少于7辆,装药品的车辆不少于4辆,那么车辆的安排有几种方案?请写出每种方案并求出最少费用.
【题目】声音在空气中传播的速度y(米/秒)是气温x (摄氏度)的一次函数,下表列出了一组不同气温时的音速.
气温x/摄氏度 | 0 | 5 | 10 | 15 | 20 |
音速y/(米/秒) | 331 | 334 | 337 | 340 | 343 |
(1)求y 与 x之间的函数关系式
(2)气温x=22(摄氏度)时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地相距多远?