题目内容
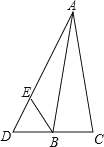
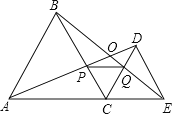
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
①AD=BE;
②PQ∥AE;
③EQ=DP;
④∠AOB=60°;
⑤当C为AE中点时,S△BPQ:S△CDE=1:3.其中恒成立的结论有( )
A.①②④B.①②③④C.①②③⑤D.①②④⑤
【答案】B
【解析】
根据等边三角形性质得出AB=BC=AC,DC=CE=DE,∠BCA=∠DCE=∠EDC=∠DEC=60°,推出∠ACD=∠BCE,根据SAS证△ACD≌△BCE,即可推出①;根据ASA证△DPC≌△EQC,推出CP=CQ,证三角形CPQ是等边三角形,即可推出②③;根据等边三角形性质和平角定义即可判断④求出P、Q分别是BC和BE中点,推出△BPQ的面积等于△BCE面积的![]() ,推出△BCE和△CDE的面积相等,即可判断⑤.
,推出△BCE和△CDE的面积相等,即可判断⑤.
∵等边△ABC和等边△DCE,
∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中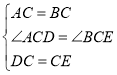 ,
,
∴△ACD≌△BCE,
∴∠CBE=∠DAC,AD=BE,∴①正确;
∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,∴④正确;
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
在△DPC和△EQC中 ,
,
∴△DPC≌△EQC,
∴EQ=DP,∴③正确;
CP=CQ,
∵∠BCD=60°,
∴△CPQ是等边三角形,
∴∠PQC=60°=∠DCE,
∴PQ∥AE,∴②正确;
∵当C为AE中点时,
∵∠BCA=∠DEC=60°,
∴P是AD中点,
∴CP=![]() DE=
DE=![]() AB,
AB,
即P是BC中点,
同理Q是BE的中点,也是DC中点,
即PQ是△BCE的中位线,
∵PQ∥AC,
∴△BPQ∽△BCE,
∴![]() ,
,
∵当C为AE中点,等边△ABC和等边△DCE,
∴BD∥AE,
即△DCE的边CE上的高和△BCE的边CE上的高相等,
∴△DEC的面积等于△BCE的面积,
∴S△BPQ:S△CDE=1:4,∴⑤错误.
正确的有①②③④.
故选:B.

 寒假乐园北京教育出版社系列答案
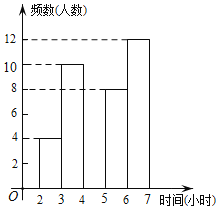
寒假乐园北京教育出版社系列答案【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?