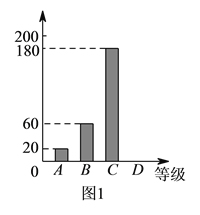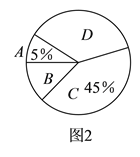题目内容
【题目】阅读：已知点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为|AB|=|a﹣b|．
理解：
（1）数轴上表示2和﹣3的两点之间的距离是 ；
（2）数轴上表示x和﹣5的两点A和B之间的距离是 ；
（3）当代数式|x﹣1|+|x+3|取最小值时，相应的x的取值范围是 ；最小值是 ．
应用：某环形道路上顺次排列有四家快递公司：A、B、C、D，它们顺次有快递车16辆，8辆，4辆，12辆，为使各快递公司的车辆数相同，允许一些快递公司向相邻公司调出，问共有多少种调配方案，使调动的车辆数最少？并求出调出的最少车辆.
【答案】（1）5；（2）|x+5|；（3）﹣3≤x≤1，4；应用：方案见解析，12辆．
【解析】试题分析：根据题意，可以求得第（1），（2），（3）的答案，根据应用的题意，可以画出五种调配方案，从而可以解答本题．
试题解析：
（1）2 和﹣3 的两点之间的距离是|2﹣（﹣3）|=5．
（2）A 和 B 之间的距离是|x﹣（﹣5）|=|x+5|．
（3）代数式|x﹣1|+|x+3|表示在数轴上到 1 和﹣3 两点的距离的和，当 x 在﹣3 和 1 之间时，代数式取得最小值，最小值是﹣3 和 1 之间的距离|1﹣（﹣3）|=4． 故当﹣3≤x≤1 时，代数式取得最小值，最小值是 4．
应用：根据题意，共有 5 种调配方案，如下图所示：
由上可知，调出的最小车辆数为：4+2+6=12 辆．
阅读快车系列答案【题目】今年入冬以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点，某校学生会为了调查学生对雾霾天气知识的了解程度，随机抽取了该校的若干名学生进行调查，将调查结果分为四个等级：（
）非常了解，（ 
）比较了解，（ 
）很少了解，（ 
）不了解，并将调查结果绘制成如下两幅不完整的统计图．
对雾霾天气了解程度的条形统计图 | 对雾霾天气了解程度的扇形统计图 |
|
|
根据统计图提供的信息，解答下列问题：
（
）求被调查的学生人数；并将条形统计图补充完整．
（
）本次调查结果的“众数”是__________．
（
）若该校有
名学生，请你估计该校对雾霾天气知识“不了解”的学生人数，并请你用一句话告诉这些学生有关雾霾的知识．
