题目内容
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 ![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+ ![]() .其中正确的结论是( )
.其中正确的结论是( ) 
A.①②③⑤
B.①②③④
C.①②③④⑤
D.①②③
【答案】A
【解析】解:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3, 又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
如图①,连接OO′,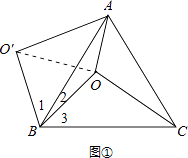
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故结论②正确;
∵△BO′A≌△BOC,∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;![]() =S△AOO′+S△OBO′=
=S△AOO′+S△OBO′= ![]() ×3×4+
×3×4+ ![]() ×42=6+4
×42=6+4 ![]() ,
,
故结论④错误;
如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.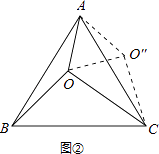
易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形,
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″= ![]() ×3×4+
×3×4+ ![]() ×32=6+
×32=6+ ![]() ,
,
故结论⑤正确.
综上所述,正确的结论为:①②③⑤.
故选:A.
证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;
由△OBO′是等边三角形,可知结论②正确;
在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;![]() =S△AOO′+S△OBO′=6+4
=S△AOO′+S△OBO′=6+4 ![]() ,故结论④错误;
,故结论④错误;
如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO″+S△AOO″ , 计算可得结论⑤正确.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】如图,某计算装置有一数据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 2 | 5 | 10 | 17 | 26 |

A.98
B.99
C.100
D.101
【题目】如表给出了某班6名同学的身高情况:(单位:cm)
(1).
同学 | A | B | C | D | E | F |
身高 | 165 | 166 | 171 | |||
身高与班级平均身高的差值 | ﹣1 | +2 | ﹣3 | +3 |
完成表中空白的部分;
(2)他们的最高身高与最矮身高相差多少?
(3)他们6人的平均身高是多少?



