题目内容
【题目】在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( ) 
A.2
B.![]()
C.![]()
D.15
【答案】C
【解析】解:设平行四边形ABCD的面积是S,设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y. 则S=5a3x=3b5y.即ax=by= ![]() .
.
△AA4D2与△B2CC4全等,B2C= ![]() BC=b,B2C边上的高是
BC=b,B2C边上的高是 ![]() 5y=4y.
5y=4y.
则△AA4D2和△B2CC4的面积是2by= ![]() .
.
同理△D2C4D与△A4BB2的面积是 ![]() .
.
则四边形A4B2C4D2的面积是S﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,即
,即 ![]() =1,
=1,
解得S= ![]() .
.
故选C.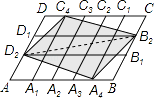
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



