Question

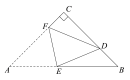
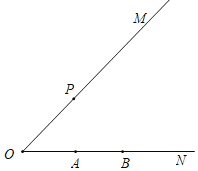
【题目】∠MON＝45°，点P在射线OM上，点A，B在射线ON上（点B与点O在点A的两侧），且AB＝1，以点P为旋转中心，将线段AB逆时针旋转90°，得到线段CD（点C与点A对应，点D与点B对应）．

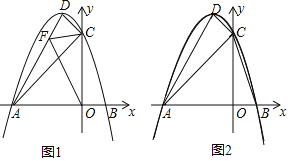
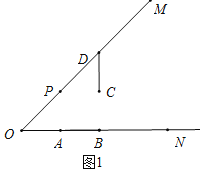
（1）如图，若OA＝1，OP，依题意补全图形；

（2）若OP，当线段AB在射线ON上运动时，线段CD与射线OM有公共点，求OA的取值范围；

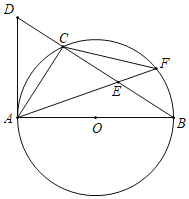
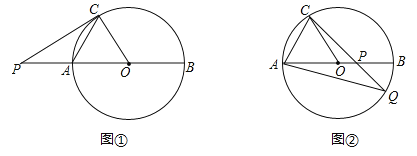
（3）一条线段上所有的点都在一个圆的圆内或圆上，称这个圆为这条线段的覆盖圆．若OA＝1，当点P在射线OM上运动时，以射线OM上一点Q为圆心作线段CD的覆盖圆，直接写出当线段CD的覆盖圆的直径取得最小值时OP和OQ的长度．

Answer 1

【答案】（1）见解析；（2）1≤OA≤2；（3）OP，OQ

【解析】

（1）利用直角三角形的性质和旋转的性质确定点C和点D的位置，连接即可得到线段CD；

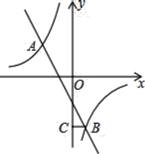
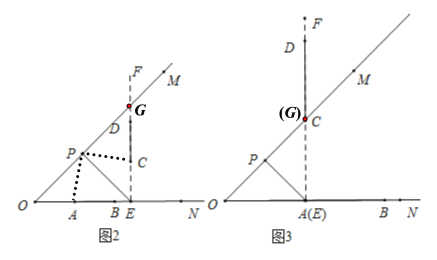
（2）如图2（见解析），作交ON于点E，作交OM于点G，利用旋转的性质、三角形全等的判定定理推出，则有，从而可得点C和点D的位置，然后结合图形，分析线段CD与射线OM有公共点时，OA的最小值与最大值即可；

（3）先确认当线段CD的覆盖圆的直径取得最小值时的直径，再利用直角三角形的性质和勾股定理求解即可.

（1）

由旋转性质可知：

是等腰直角三角形

∴D正好落在OM上

因此，补全图形如图1所示；

（2）如图2，作交ON于点E，作交OM于点G

连接PA、PC

由旋转的性质得：

则点C在射线EF上

同理可证：点D也在射线EF上

因此，当线段AB在射线ON上从左向右平移时，线段CD在射线EF上从下向上平移，且

当点D与点G重合时，OA取得最小值，由（1）可知，最小值为

如图3，当点C与点G重合时，OA取得最大值，最大值为

综上，OA的取值范围是；

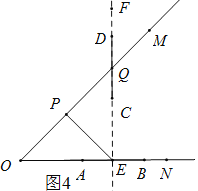
（3）如图4．作PE⊥OM交ON于点E，作EF⊥ON交OM于点Q

当线段CD的覆盖圆的直径取得最小值时，直径为

则圆心点Q为CD的中点，

由（2）可知

在中，

则

在中，

则，解得

故的长度为，的长度为.