题目内容
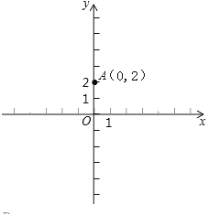
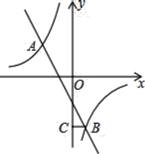
【题目】如图,在平面直角坐标系中,双曲线![]() 和直线
和直线![]() 交于A,B两点,点A的坐标为
交于A,B两点,点A的坐标为![]() ,
,![]() 轴于点C,且
轴于点C,且![]() .
.
![]() 求双曲线和直线的解析式;
求双曲线和直线的解析式;
![]() 求
求![]() 的面积.
的面积.
![]() 直接写出不等式
直接写出不等式![]() 的解集.
的解集.
【答案】(1)双曲线的解析式为:y=-![]() ,直线的解析式为:y=-2x-4;(2)8;(3)-3<x<0或x>1.
,直线的解析式为:y=-2x-4;(2)8;(3)-3<x<0或x>1.
【解析】
(1)先把A点坐标代入![]() 求出m,从而得到反比例函数解析式;再利用OC=6BC可设B点坐标为(t,-6t)(t>0),然后把B(t,-6t)代入反比例函数解析式求出t,得到B点坐标为(1,-6),再利用待定系数法求一次函数解析式;
求出m,从而得到反比例函数解析式;再利用OC=6BC可设B点坐标为(t,-6t)(t>0),然后把B(t,-6t)代入反比例函数解析式求出t,得到B点坐标为(1,-6),再利用待定系数法求一次函数解析式;
(2)先确定直线y=-2x-4与x轴的交点D的坐标,然后根据三角形面积公式和△AOB的面积=S△AOD+S△BOD进行计算;
(3)根据一次函数与反比例函数的两交点A与B的横坐标,以及0,将x轴分为四个范围,找出反比例图象在一次函数图象上方时x的范围即可.
(1)∵点A(-3,2)在双曲线![]() 上,
上,
∴2=![]() ,即m=-6,
,即m=-6,
∴双曲线的解析式为:y=-![]() ,
,
∵点B在双曲线y=-![]() 上,且OC=6BC,设点B的坐标为(a,-6a),
上,且OC=6BC,设点B的坐标为(a,-6a),
∴-6a=-![]() ,
,
解得:a=±1(负值舍去),
∴点B的坐标为(1,-6),
∵直线y=kx+b过点A,B,
∴![]() ,
,
解得:![]() ,
,
∴直线的解析式为y=-2x-4;
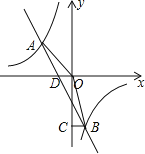
(2)直线y=-2x-4交x轴于点D,如图,
把y=0代入y=-2x-4得-2x-4=0,
解得x=-2,
则D点坐标为(-2,0),
△AOB的面积=S△AOD+S△BOD
=![]() ×2×2+
×2×2+![]() ×2×6
×2×6
=8.
(3)根据图象得:不等式![]() >kx+b的解集为-3<x<0或x>1.
>kx+b的解集为-3<x<0或x>1.

 阅读快车系列答案
阅读快车系列答案【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?