题目内容
【题目】已知抛物线y＝ax2+bx+3与x轴分别交于点A(﹣3，0)，B(1，0)交于点C，抛物线的顶点为点D．
（1）抛物线的表达式及顶点D的坐标．
（2）若点F是线段AD上一个动点，
①如图1，当FC+FO的值最小时，求点F的坐标；
②如图2，以点A，F，O为顶点的三角形能否与△ABC相似？若能，求出点F的坐标；若不能，请说明理由．
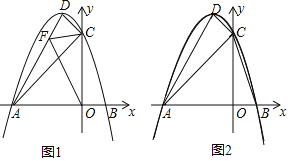
【答案】（1）y＝﹣x2﹣2x+3，(﹣1，4)；（2）①F(﹣
，3)，②能，(﹣
，
)或(﹣2，2)
【解析】
（1）抛物线的表达式为：y＝a（x+3）（x﹣1）＝a（x2+2x﹣3），故﹣3a＝3，解得：a＝﹣1，即可求解；再将抛物线解析式化为顶点式即可得出点D的坐标；
（2）①点D的坐标为：（﹣1，4），点A（﹣3，0），点C（0，3），作点O关于直线AD的对称轴R，连接CR交AD于点F，则点F为所求点，即可求解；
②当∠AOF＝∠ABC时，△AOF∽△CBA，OF∥BC，直线BC的解析式为y＝﹣3x+3，直线OF的解析式为y＝﹣3x，直线AD的解析式为y＝2x+6，联立直线OF、AD的表达式并解得：x＝﹣，故点F（﹣，）；当∠AOF＝∠CAB＝45°时，△AOF∽△CAB，∠CAB＝45°，OF⊥AC，直线OF的解析式为y＝﹣x，将上式与y＝2x+6联立并解得：x＝﹣2，即可求解．
解：（1）抛物线的表达式为：y＝a（x+3）（x﹣1）＝a（x2+2x﹣3），
故﹣3a＝3，
解得：a＝﹣1，
故抛物线的表达式为：y＝﹣x2﹣2x+3；
点D的坐标为（﹣1，4）
（2）①点D的坐标为：（﹣1，4），点A（﹣3，0），点C（0，3），
作点O关于直线AD的对称轴R，连接CR交AD于点F，则点F为所求点，
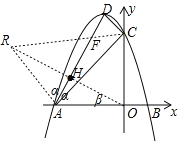
FC+FO＝FC+RF＝CR为最小，
连接AR，设直线OR交AD于点H，
由点A、D的坐标得，直线AD的表达式为：y＝2x+6，
则tan∠DAO＝2＝tanα，
设∠HOA＝∠β，则tanβ＝
，则cosβ＝
，sinβ＝
，
OH＝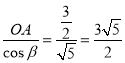
，OR＝2OH＝3
，
yR＝ORsinβ＝3×＝3＝yC，
故RC∥x轴，
故yF＝3＝2x+6，x＝﹣，
则点F（﹣，3）；
②在Rt△ACD中，tan∠CAD
，
在Rt△OBC中，tan∠OCB＝
，
∴∠ACD＝∠OCB，
∵OA＝OC，
∴∠OAC＝∠OCA＝45°，
∴∠FAO＝∠ACB，
若以A，F，O为顶点的三角形与△ABC相似，则可分两种情况考虑：
当∠AOF＝∠ABC时，△AOF∽△CBA，
∴OF∥BC，
设直线BC的解析式为y＝kx+b，
将点B、C的坐标代入上式并解得：
直线BC的解析式为y＝﹣3x+3，
∴直线OF的解析式为y＝﹣3x，
直线AD的解析式为y＝2x+6，
联立直线OF、AD的表达式，
解得：x＝﹣，故点F（﹣，）：；
当∠AOF＝∠CAB＝45°时，△AOF∽△CAB，
∵∠CAB＝45°，
∴OF⊥AC，
∴直线OF的解析式为y＝﹣x，
将上式与y＝2x+6联立并解得：x＝﹣2，
故点F（﹣2，2）；
综合以上可得F点的坐标为（﹣，）或（﹣2，2）．
