题目内容
正比例函数y=k1x和反比例函数y=
(k1k2≠0)的图象交于点A(-0.5,2)和点B.求点B的坐标.
| k2 | x |
分析:将A坐标代入正比例函数解析式中求出k1的值,代入反比例解析式中求出k2的值,分别确定出两函数解析式,联立两函数解析式,即可求出B的坐标.
解答:解:∵正比例函数y=k1x和反比例函数y=
(k1k2≠0)的图象交于点A(-0.5,2),
∴将x=-0.5,y=2代入正比例解析式得:k1=
=-4,代入反比例解析式得:k2=-0.5×2=-1;
∴
,
解得:
或
,
∴B(0.5,-2).
| k2 |
| x |
∴将x=-0.5,y=2代入正比例解析式得:k1=
| 2 |
| -0.5 |
∴
|
解得:
|
|
∴B(0.5,-2).
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,灵活运用待定系数法是解本题的关键.

练习册系列答案
相关题目
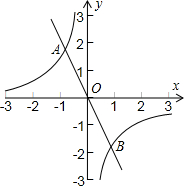 (2012•广州)如图,正比例函数y1=k1x和反比例函数y2=
(2012•广州)如图,正比例函数y1=k1x和反比例函数y2=