题目内容
22、已知正比例函数y=k1x（k1≠0）的图象经过A（3，-6）、B（m，2）两点．
（1）求m的值；
（2）如果点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C共有多少个？（请直接写出点C的个数）
（1）求m的值；
（2）如果点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C共有多少个？（请直接写出点C的个数）
分析：（1）把A坐标代入正比例函数可得k1的值，把B的坐标代入一次函数可得B的值；
（2）分别让任意两边当腰，数出C的个数即可．
（2）分别让任意两边当腰，数出C的个数即可．
解答：解：（1）∵-6=3k1（1分）
∴k1=-2（1分）
又k1m=2（1分）
∴m=-1（11分）
（2）分别以点A，B为圆心，AB长为半径画弧，可得与坐标轴的交点共8个，进而作出AB的垂直平分线，交坐标轴于两点，
∴点C共有10个．（2分）
∴k1=-2（1分）
又k1m=2（1分）
∴m=-1（11分）
（2）分别以点A，B为圆心，AB长为半径画弧，可得与坐标轴的交点共8个，进而作出AB的垂直平分线，交坐标轴于两点，
∴点C共有10个．（2分）
点评：考查一次函数的应用；用到的知识点为：正比例函数上点的横纵坐标适合正比例函数解析式；等腰三角形的两腰不确定的情况下，可分3种情况探讨．
练习册系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
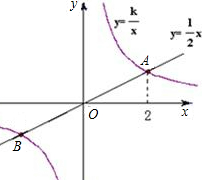
横坐标为2．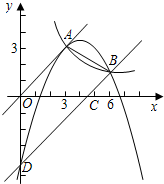
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．