题目内容
已知正△ABC的面积是1，P是△ABC内一点，并且△PAB、△PBC、△PCA的面积相等，那么满足条件的点P共有______个；△PAB的面积是______．
∵△PAB、△PBC、△PCA的面积相等，AB=BC=AC，
∴P到AB、BC、AC的距离相等，
故点P为等边三角形三角平分线的交点，
等边三角形三角平分线交于一点，
故点P只有一个，
且△PAB的面积为
．
故答案为：1，
．
∴P到AB、BC、AC的距离相等，
故点P为等边三角形三角平分线的交点，
等边三角形三角平分线交于一点，
故点P只有一个，
且△PAB的面积为
| 1 |
| 3 |
故答案为：1，
| 1 |
| 3 |
练习册系列答案
相关题目
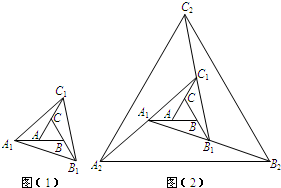（2011•成华区二模）如图（1），已知正△ABC的面积为1，把它的各边延长一倍得到正△A1B1C1；再把△A1B1C1的各边延长一倍得到正△A2B2C2（如（2））；…；如此下去，则正△AnBnCn的面积为
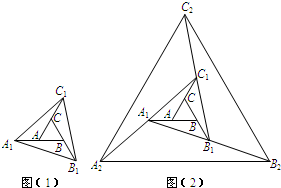如图（1），已知正△ABC的面积为1，把它的各边延长一倍得到正△A1B1C1；再把△A1B1C1的各边延长一倍得到正△A2B2C2（如（2））；…；如此下去，则正△AnBnCn的面积为______．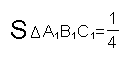
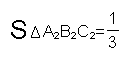， 则 
，则
； 
，则 
；
, 则
（ ）