题目内容
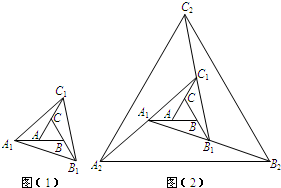 (2011•成华区二模)如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为
(2011•成华区二模)如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为7n
7n
.分析:先根据已知条件求出△A1B1C1及△A2B2C2的面积,再根据两三角形的倍数关系求解即可.
解答:解:△ABC与△A1BB1底相等(AB=A1B),高为1:2(BB1=2BC),故面积比为1:2,
∵△ABC面积为1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证S△A2B2C2=7S△A1B1C1=49,
∴如此下去,则正△AnBnCn的面积=7n.
故答案为:7n.
∵△ABC面积为1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证S△A2B2C2=7S△A1B1C1=49,
∴如此下去,则正△AnBnCn的面积=7n.
故答案为:7n.
点评:本题考查的是等边三角形的性质及三角形的面积,根据题意得出S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7,S△A2B2C2=7S△A1B1C1=49,找出规律是解答此题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
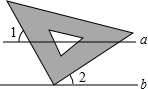 (2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( )
(2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( )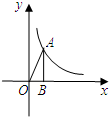 (2011•成华区二模)如图,已知点A是双曲线
(2011•成华区二模)如图,已知点A是双曲线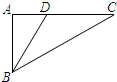 (2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )
(2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )