题目内容
已知正△ABC的面积是1,P是△ABC内一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有分析:根据三角形面积的计算和△PAB、△PBC、△PCA的面积相等可得P到AB、BC、AC的距离相等,故P点为等边三角形三个角平分线的交点,故P点只有一个,且△PAB的面积为等边△ABC面积的
.
| 1 |
| 3 |
解答:解:∵△PAB、△PBC、△PCA的面积相等,AB=BC=AC,
∴P到AB、BC、AC的距离相等,
故点P为等边三角形三角平分线的交点,
等边三角形三角平分线交于一点,
故点P只有一个,
且△PAB的面积为
.
故答案为:1,
.
∴P到AB、BC、AC的距离相等,
故点P为等边三角形三角平分线的交点,
等边三角形三角平分线交于一点,
故点P只有一个,
且△PAB的面积为
| 1 |
| 3 |
故答案为:1,
| 1 |
| 3 |
点评:本题考查了等边三角形各边长相等的性质,三角形面积的计算,本题中求得P点是等边三角形三个角平分线的交点是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
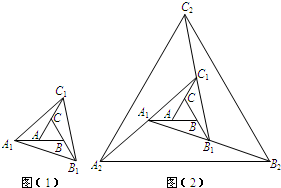 (2011•成华区二模)如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为
(2011•成华区二模)如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为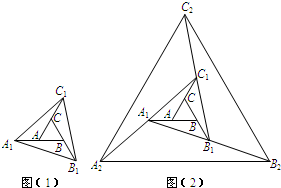 如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为______.
如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为______.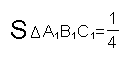
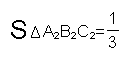 ;
;  ;
;