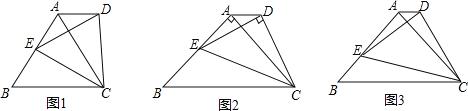
题目内容
【题目】某地下车库出口处“两段式栏杆”如图①所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图②所示,其示意图如图③所示,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2m.现有一高度为2.4m的货车要送货进入地下车库,问此货车能否安全通过?请通过计算说明.(栏杆宽度忽略不计,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

【答案】此货车不能安全通过.
【解析】
过E作ED⊥BC于D,AG⊥ED于G,求出DE的长与2.4比较即可判断.
过E作ED⊥BC于D,AG⊥ED于G,
则∠AEG=37°,DG=AB=1.2m,EG=AEcos37°=1.2×0.80=0.96m,
∴ED=EG+DG=1.2+0.96=2.16m<2.4m,
故此货车不能安全通过.
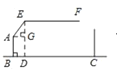

 黄冈天天练口算题卡系列答案
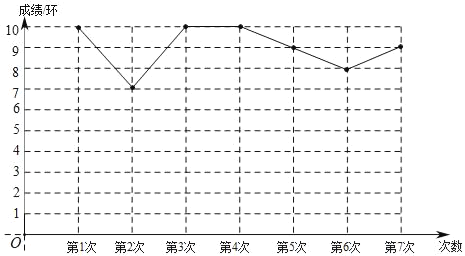
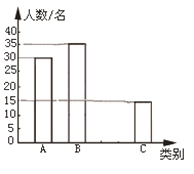
黄冈天天练口算题卡系列答案【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
【题目】大学生小亮响应国家创新创业号召,回家乡承包了一片坡地,改造后种植优质猕猴桃.经核算这批猕猴桃的种植成本为16 元![]() ,设销售时间为
,设销售时间为![]() (天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元
(天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元![]() )与时间x(天)的关系:当
)与时间x(天)的关系:当![]() 时,p与x满足一次函数关系,如下表:
时,p与x满足一次函数关系,如下表:
| 2 | 4 | 6 | ...... |
| 35 | 34 | 33 | ...... |
当![]() 时,销售价格稳定为24元
时,销售价格稳定为24元![]() ;②猕猴桃的销售量
;②猕猴桃的销售量![]() 与时间
与时间![]() (天)之间的关系:第一天卖出
(天)之间的关系:第一天卖出![]() ,以后每天比前一天多卖出
,以后每天比前一天多卖出![]() .
.
(1)填空:试销的一个月中,销售价p(元![]() )与时间
)与时间![]() (天)的函数关系式为____;销售量
(天)的函数关系式为____;销售量![]() 与时间x(天)的函数关系式为_____.
与时间x(天)的函数关系式为_____.
2)求销售第几天时,当天的利润最大?最大利润是多少?
(3)请求出试销的一个月中当天销售利润不低于 930 元的天数.