题目内容
【题目】如图所示是反比例函数![]() 的图象的一支。根据图象回答下列问题:
的图象的一支。根据图象回答下列问题:
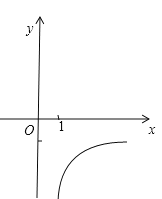
(1)图象的另一支在哪个象限?常数k的取值范围是什么?
(2)在这个函数图象的某一支上任意取两点![]() 和
和![]() 。如果
。如果![]() ,那么
,那么![]() 和
和![]() 有怎样的大小关系?
有怎样的大小关系?
(3)在函数![]() 的图象上任意取两点
的图象上任意取两点![]() 和
和![]() ,且
,且![]() ,那么
,那么![]() 和
和![]() 的大小关系又如何?
的大小关系又如何?
【答案】(1)第二象限,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据反比例函数y=![]() (k≠0)的性质知,当k<0,该函数的图象经过第二、四象限;
(k≠0)的性质知,当k<0,该函数的图象经过第二、四象限;
(2)根据反比例函数的性质解答;
(3)根据反比例函数图象上点的坐标特征,将A(x1,y1)和B(x2,y2)代入函数y=![]() ,求得y1和y2的符号,然后比较它们的大小即可.
,求得y1和y2的符号,然后比较它们的大小即可.
(1)由反比例函数的对称性,知图象的另一支在第二象限;
根据反比例函数的性质,知1-2k<0,
解得,k>![]() ;
;
(2)由该函数图象的性质知,当反比例函数y=![]() 经过第二、四象限时,该函数在任意一支上y随x的增大而增大,
经过第二、四象限时,该函数在任意一支上y随x的增大而增大,
∴当x1<x2时,y1<y2;
(3)由(1)知1-2k<0,
∵x1<0<x2,
∴y1=![]() >0,y2=
>0,y2=![]() <0,
<0,
∴y1>y2.

练习册系列答案
相关题目