题目内容
已知y=ax2+bx+c(a≠0)图象与直线y=kx+4相交于A(1,m),B(4,8)两点,与x轴交于原点及点C.
(1)求直线和抛物线解析式;
(2)在x轴上方的抛物线上是否存在点D,使S△OCD=2S△OAB?如果存在,求出点D坐标,如果不存在,说明理由.
解:(1)∵直线y=kx+4过A(1,m),B(4,8)两点,
∴ ,解得
,解得 ,∴y=x+4,
,∴y=x+4,
把O、A、B三点坐标代入抛物线解析式,得 ,
, ,
,
∴y=-x2+6x;
(2)存在.设D点纵坐标为h(h>0),
由O(0,0),A(1,5),B(4,8),可知S△OAB=6,
∴S△OCD=2S△OAB=12, ×6×h=12,解得h=4,
×6×h=12,解得h=4,
由-x2+6x=4,得x=3± ,
,
∴D(3+ ,4)或(3-
,4)或(3- ,4).
,4).
分析:(1)由直线y=kx+4过A(1,m),B(4,8)两点,列方程组求k、m的值,再把O、A、B三点坐标代入抛物线解析式求a、b、c的值;
(2)存在.根据O、A、B三点坐标求△OAB的面积,再由S△OCD=2S△OAB=12,求D点纵坐标,代入抛物线解析式求D点纵坐标.
点评:本题考查了二次函数的综合运用.关键是根据已知条件求两函数解析式,再根据面积的等量关系求D的坐标.
∴
 ,解得
,解得 ,∴y=x+4,
,∴y=x+4,把O、A、B三点坐标代入抛物线解析式,得
 ,
, ,
,∴y=-x2+6x;
(2)存在.设D点纵坐标为h(h>0),
由O(0,0),A(1,5),B(4,8),可知S△OAB=6,
∴S△OCD=2S△OAB=12,
 ×6×h=12,解得h=4,
×6×h=12,解得h=4,由-x2+6x=4,得x=3±
 ,
,∴D(3+
 ,4)或(3-
,4)或(3- ,4).
,4).分析:(1)由直线y=kx+4过A(1,m),B(4,8)两点,列方程组求k、m的值,再把O、A、B三点坐标代入抛物线解析式求a、b、c的值;
(2)存在.根据O、A、B三点坐标求△OAB的面积,再由S△OCD=2S△OAB=12,求D点纵坐标,代入抛物线解析式求D点纵坐标.
点评:本题考查了二次函数的综合运用.关键是根据已知条件求两函数解析式,再根据面积的等量关系求D的坐标.

练习册系列答案
相关题目
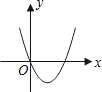 已知y=ax2+bx+c的图象如图所示,则y=ax+b的图象一定过( )
已知y=ax2+bx+c的图象如图所示,则y=ax+b的图象一定过( )| A、第一,二,三象限 | B、第一,二,四象限 | C、第二,三,四象限 | D、第一,三,四象限 |
 已知y=ax2+bx+c的图象如图,那么关于x的方程ax2+bx+c-3=0的根的情况( )
已知y=ax2+bx+c的图象如图,那么关于x的方程ax2+bx+c-3=0的根的情况( )