题目内容
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥ AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形, 保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为![]() ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角
形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
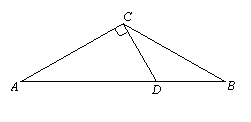
解:(1)作出圆心O,
以点O为圆心,OA长为半径作圆
(2)证明:∵CD⊥AC,∴∠ACD=90°.
∴AD是⊙O的直径
连结OC,∵∠A=∠B=30°,
∴∠ACB=120°,又∵OA=OC,
∴∠ACO=∠A =30°,
∴∠BCO=∠ACB-∠ACO =120°-30°=90°.
∴BC⊥OC,
∴BC是⊙O的切线.

(3)存在.
∵∠BCD=∠ACB-∠ACD=120°-90°=30°,
∴∠BCD=∠B, 即DB=DC.
又∵在Rt△ACD中,DC=AD![]() , ∴BD=
, ∴BD= ![]() .
.
解法一:①过点D作DP1// OC,则△P1D B∽△COB, ![]() ,
,
∵BO=BD+OD=![]() ,
,
∴P1D=![]() ×OC=
×OC=![]() ×
×![]() =
=![]() .
.
②过点D作DP2⊥AB,则△BDP2∽△BCO, ∴![]() ,
,
∵BC=![]()
∴![]() .
.
解法二:①当△B P1D∽△BCO时,∠DP1B=∠OCB=90°.
在Rt△B P1D中,
DP1=![]() .
.
②当△B D P2∽△BCO时,∠P2DB=∠OCB=90°.
在Rt△B P2D中,
DP2=![]() .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
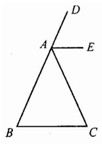 21、如图,已知在等腰三角形ABC中,AB=AC,AE∥BC.求证:AE平分∠DAC.
21、如图,已知在等腰三角形ABC中,AB=AC,AE∥BC.求证:AE平分∠DAC.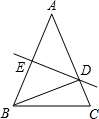 如图,已知在等腰△ABC中,如果AB=AC,∠A=40°,DE是AB的垂直平分线,那么∠DBC=
如图,已知在等腰△ABC中,如果AB=AC,∠A=40°,DE是AB的垂直平分线,那么∠DBC=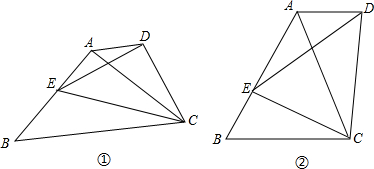
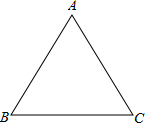 如图,已知在等腰△ABC中,AB=AC=13,BC=10,求底角∠B的三角函数值.
如图,已知在等腰△ABC中,AB=AC=13,BC=10,求底角∠B的三角函数值.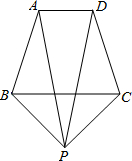 如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?
如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?