题目内容

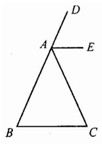21、如图，已知在等腰三角形ABC中，AB=AC，AE∥BC．求证：AE平分∠DAC．

分析：根据等腰三角形的性质，两底角相等，以及平行线的性质，内错角相等，和三角形的外角等于不相邻的两内角的和即可求证．

解答：证明：∵AB=AC，
∴∠B=∠C，
∵AE∥BC，
∴∠C=∠EAD，
又∵∠DAC=∠A+∠B=∠EAD+∠EAC，
∴∠DAE=∠EAC，
∴AE平分∠DAC．

点评：本题主要考查了等腰三角形的性质，以及平行线的性质，正确应用等腰三角形的性质是解题的关键．

练习册系列答案

课外作业系列答案

教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.

类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时

sad A=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.

根据上述对角的正对定义，解下列问题：

（1）sad 的值为（ ▼ ）

A. B.1 C. D.2

（2）对于，∠A的正对值sad A的取值范围是 ▼ .

（3）已知，其中为锐角，试求sad的值.

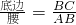通过学习锐角三角比，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此，两条边长的比值与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对（can），如图（1）在△ABC中，AB=AC，底角B的邻对记作canB，这时canB= $数学公式$ ，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义，解下列问题：
（1）can30°=______；
（2）如图（2），已知在△ABC中，AB=AC，canB= $数学公式$ ，S_△ABC=24，求△ABC的周长．

如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥ AC交AB于点D.

(1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；

(2)求证：BC是过A，D，C三点的圆的切线；

(3)若过A，D，C三点的圆的半径为,则线段BC上是否存在一点P，使得以P，D，B为顶点的三角

形与△BCO相似.若存在，求出DP的长；若不存在，请说明理由.

试题分类