题目内容
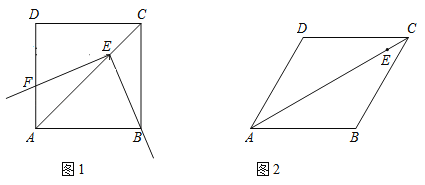
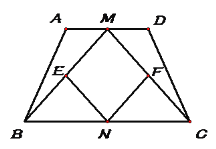
【题目】如图，在等腰梯形ABCD中，AB=DC，点M，N分别是AD，BC的中点，点E，F分别是BM，CM的中点． （1）求证：四边形MENF是菱形； （2）当四边形MENF是正方形时，求证：等腰梯形ABCD的高是底边BC的一半．
【答案】见解析
【解析】
（1）利用等腰梯形的性质证明
，利用全等三角形性质及中点概念，中位线的性质证明四边形
的四边相等得结论．（2）连接
，利用三线合一证明是等腰梯形的高，再利用正方形与直角三角形的性质可得结论．
（1）
四边形
为等腰梯形，
所以
，
为
中点，
．
，
．
为
、
中点，
，
，
所以：
，
为
的中点，为
中点
，
∴四边形
是菱形．
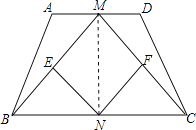
（2）连结MN， ∵BM=CM，BN=CN，
∴MN⊥BC， ∵AD∥BC， ∴MN⊥AD，
∴MN是梯形ABCD的高，
又∵四边形MENF是正方形，
∴△BMC为直角三角形，
又∵N是BC的中点，
，
即等腰梯形ABCD的高是底边BC的一半．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
