Question

如图有两个可自由转动的转盘，A转盘被平均分成2个相等的扇形区域，分别标注数字1和2；B转盘被平均分成3个相等的扇形区域，分别标注数字-1，-2，-3．分别转动这两个转盘，将A盘所得结果记为x，B盘所得结果记为y，这样就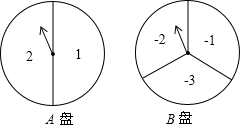确定了点P的坐标（x，y），
（1）用列表或树状图法写出点P的所有可能性；
（2）求点P落在双曲线y=-

2

x

上的概率．

Answer 1

（1）列表得：

A盘（x） B盘（y）	1	2
-1	（1，-1）	（2，-1）
-2	（1，-2）	（2，-2）
-3	（1，-3）	（2，-3）

或画树状图得：

则点P的所有可能性有：（1，-1），（1，-2），（1，-3），（2，-1），（2，-2），（2，-3）；

（2）∵点P落在双曲线y=-

2

x

上的有（1，-2）与（2，-1）两种情况，
∴点P落在y=-

2

x

上的概率为：

2

6

=

1

3

．