题目内容
【题目】定义:在平面直角坐标系xOy中,如果将点P绕点T(0,t)(t>0)旋转180°得到点Q,那么称线段QP为“拓展带”,点Q为点P的“拓展点”.
(1)当t=3时,点(0,0)的“拓展点”坐标为 ,点(﹣1,1)的“拓展点”坐标为 ;
(2)如果 t>1,当点M(2,1)的“拓展点”N在函数y=﹣![]() 的图象上时,求t的值;
的图象上时,求t的值;
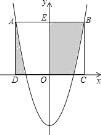
(3)当t=1时,点Q为点P(2,0)的“拓展点”,如果抛物线 y=(x﹣m)2﹣1与“拓展带”PQ有交点,求m的取值范围.
【答案】(1)(0,6),(1,5);(2)![]() ;(3)m的取值范围为
;(3)m的取值范围为![]() .
.
【解析】
(1)根据中心对称可得结果;
(2)把点M坐标带入反比例函数解析式即可得解;
(3)因为抛物线![]() 与“拓展带”PQ有交点,所以将点P、Q坐标以分别代入解析式即可解答.
与“拓展带”PQ有交点,所以将点P、Q坐标以分别代入解析式即可解答.
(1)点(0,0)的“拓展点”坐标为(0,6),点(-1,1)的“拓展点”坐标为(1,5).
(2)当t>1时,点M(2,1)的“拓展点”N为(-2,2t-1).
∵点N在函数![]() 的图象上,
的图象上,
∴![]() .
.
∴![]() .
.
(3)当t=1时,点P(2,0)的“拓展点”Q为(-2,2),
当抛物线![]() 经过点P(2,0)时,可得
经过点P(2,0)时,可得![]() 或
或![]() .
.
当抛物线![]() 经过点Q(-2,2)时,可得
经过点Q(-2,2)时,可得![]() 或
或![]() .
.
∴m的取值范围为![]() .
.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目