题目内容
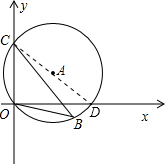
如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )

A.
| B.
| C.
| D.
|

连接CD,如图所示:
∵∠COD=90°,
∴CD为圆A的直径,即CD过圆心A,
又∵∠CBO与∠CDO为
所对的圆周角,
∴∠CBO=∠CDO,
又∵C(0,5),
∴OC=5,
在Rt△CDO中,CD=10,CO=5,
根据勾股定理得:OD=
=5
,
∴cos∠CBO=cos∠CDO=
=
=
.
故选B
∵∠COD=90°,
∴CD为圆A的直径,即CD过圆心A,
又∵∠CBO与∠CDO为
 |
| CO |
∴∠CBO=∠CDO,
又∵C(0,5),
∴OC=5,
在Rt△CDO中,CD=10,CO=5,
根据勾股定理得:OD=
| CD2-OC2 |
| 3 |
∴cos∠CBO=cos∠CDO=
| OD |
| CD |
5
| ||
| 10 |
| ||
| 2 |
故选B


练习册系列答案
相关题目








