题目内容
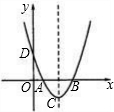 如图,在直角坐标系中,二次函数的顶点为C(4,-3),且在x轴上截得的线段AB=6,则二次函数的表达式为
如图,在直角坐标系中,二次函数的顶点为C(4,-3),且在x轴上截得的线段AB=6,则二次函数的表达式为分析:由于二次函数的顶点为C(4,-3),可用顶点式设此函数的解析式是y=a(x-4)2-3;再根据二次函数的轴对称性,结合已知条件在x轴上截得的线段AB=6,知此函数与x轴的交点A、B坐标,然后把A或者B点的坐标代入,即可求出此函数的解析式;
由于四边形DACB的面积=S=S△ABC+S△ABD,而A、B、C三点的坐标都知道,故只需求出D点的坐标,而D是抛物线与y轴的交点,把x=0代入二次函数的表达式即可.
由于四边形DACB的面积=S=S△ABC+S△ABD,而A、B、C三点的坐标都知道,故只需求出D点的坐标,而D是抛物线与y轴的交点,把x=0代入二次函数的表达式即可.
解答:解:二次函数的顶点为C(4,-3),因而函数的对称轴是:x=4
线段AB=6,则A,B点的坐标是(1,0)和(7,0)
设函数的解析式是y=a(x-4)2-3
把点(1,0)代入
就可以求出解析式是:y=
(x-4)2-3
即二次函数的表达式为y=
x2-
x+
在解析式中令x=0,解得D点的坐标是(0,
)
∴四边形DACB的面积=S=S△ABC+S△ABD=
AB•3+
AB•
=16.
线段AB=6,则A,B点的坐标是(1,0)和(7,0)
设函数的解析式是y=a(x-4)2-3
把点(1,0)代入
就可以求出解析式是:y=
| 1 |
| 3 |
即二次函数的表达式为y=
| 1 |
| 3 |
| 8 |
| 3 |
| 7 |
| 3 |
在解析式中令x=0,解得D点的坐标是(0,
| 7 |
| 3 |
∴四边形DACB的面积=S=S△ABC+S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 3 |
点评:当已知函数的顶点坐标,或已知函数对称轴时,利用顶点式求解析式比较简单;当已知图象经过的三点时,一般利用一般式求解.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目

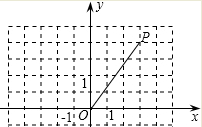 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
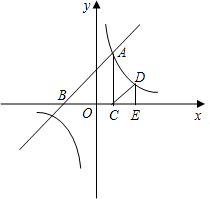
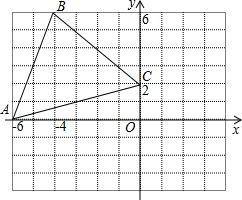 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: