题目内容
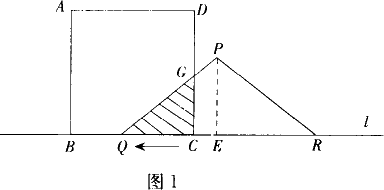
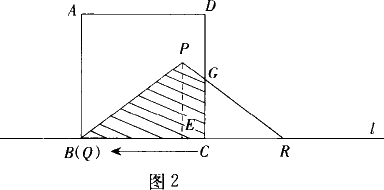
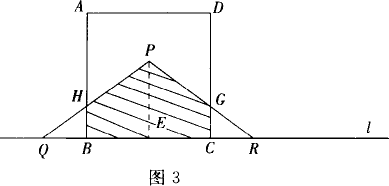
如图,有一个边长为5 cm的正方形ABCD和等腰△PQR,PQ=PR=5 cm,QR=8 cm,点B、C、Q、R在同一条直线l上,当C、Q两点重合时,等腰三角形PQR以1 cm/秒的速度沿直线l按箭头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合的部分为Scm2,解答下列各问题:
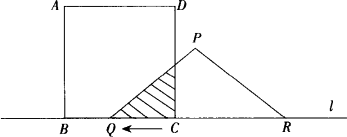
(1)当t=3秒时,求S值;
(2)t=5秒时,求S的值;
(3)当5秒≤t≤8秒时,求S与t之间的函数关系式,并求出S的最大值.
答案:
解析:
解析:
|
(2)当t=5时,CR=3(图2), 设PR交DC于G, 由△RCG∽△REP可求出S△RCG= ∴S△PBR-S△RCG=12- (3)当5≤t≤8时,RC=8-t(图3), 设PQ交AB于H, 由△QBH∽△QEP得 S△QBH= 由△RCG∽△REP得S△RCG= ∴S=12- 即 S=- 当t= 抓住△PQR运动过程中与正方形ABCD重合部分面积的变化关系,用“静”的观点研究“动”,有效地解决了问题. 解决运动问题,要领会“动”中“静”的问题本质,“静”时必含有两个数值间的定量关系,“动”时则体现两个变量之间的函数关系.用“静”的观点研究“动”,是解决动态问题的重要思想. |

练习册系列答案
相关题目
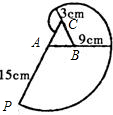 如图,有一个边长为6cm的正三角形ABC木块,点P是边CA的延长线上的点,在A、P之间拉一条细绳,绳长AP为15cm.握住点P,拉直细绳,把它全部紧紧缠绕在△ABC木块上(缠绕时木块不动),若圆周率取3.14,点P运动的路线长为( )(精确到0.1cm)
如图,有一个边长为6cm的正三角形ABC木块,点P是边CA的延长线上的点,在A、P之间拉一条细绳,绳长AP为15cm.握住点P,拉直细绳,把它全部紧紧缠绕在△ABC木块上(缠绕时木块不动),若圆周率取3.14,点P运动的路线长为( )(精确到0.1cm)| A、28.3cm | B、28.2cm | C、56.5cm | D、56.6cm |
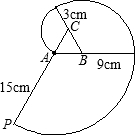 如图,有一个边长为6cm的正三角形木块ABC,点P是CA延长线上的一点,在A、P之间拉一条长为15cm细丝,握住点P,拉直细线,把它全部紧紧绕在△ABC木块上(缠绕时木块不动),则点P运动的路线长为(π取3.14,精确到0.1cm)( )
如图,有一个边长为6cm的正三角形木块ABC,点P是CA延长线上的一点,在A、P之间拉一条长为15cm细丝,握住点P,拉直细线,把它全部紧紧绕在△ABC木块上(缠绕时木块不动),则点P运动的路线长为(π取3.14,精确到0.1cm)( )| A、28.3cm | B、28.2cm | C、56.5cm | D、56.6cm |

 20、如图,有一个边长为5的正方形纸片ABCD,要将其剪拼成边长分别为a,b的两个小正方形,使得a2+b2=52.
20、如图,有一个边长为5的正方形纸片ABCD,要将其剪拼成边长分别为a,b的两个小正方形,使得a2+b2=52. 19、如图,有一个边长为5的正方形纸片ABCD,要将其剪拼成边长分别为a,b的两个小正方形,使得a2+b2=52.①a,b的值可以是
19、如图,有一个边长为5的正方形纸片ABCD,要将其剪拼成边长分别为a,b的两个小正方形,使得a2+b2=52.①a,b的值可以是 10、如图,有一个边长为6cm的正三角形,从它的三个角截去三个小等边三角形后得到一个正六边形,则正六边形的边长为
10、如图,有一个边长为6cm的正三角形,从它的三个角截去三个小等边三角形后得到一个正六边形,则正六边形的边长为