题目内容
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
【答案】
(1)100;108°
(2)解:如图所示: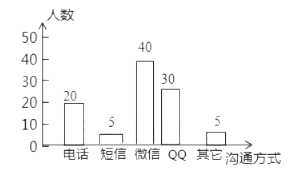
(3)解:喜欢用微信沟通所占百分比为: ![]() ×100%=40%,
×100%=40%,
∴该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有:1500×40%=600人;
(4)解:列出树状图,如图所示: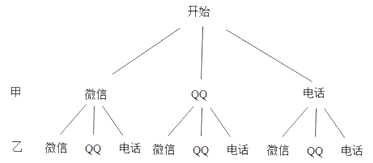
所有情况共有9种情况,其中两人恰好选中同一种沟通方式共有3种情况,甲、乙两名同学恰好选中同一种沟通方式的概率为: ![]() =
= ![]() .
.
【解析】(1)喜欢用电话沟通的人数为20,所占百分比为20%,∴此次共抽查了:20÷20%=100人,喜欢用QQ沟通所占比例为: ![]() =
= ![]() ,
,
∴QQ”的扇形圆心角的度数为:360°× ![]() =108°;
=108°;
(2)喜欢用短信的人数为:100×5%=5人,喜欢用微信的人数为:100﹣20﹣5﹣30﹣5=40.
补充图形,如图所示:
(1)共抽查的学生=电话的人数除以电话所占的百分比;表示“QQ”的扇形圆心角的度数=360°乘以“QQ”所占百分比,计算即可得出答案。
(2)分半求出喜欢用短信的人数和喜欢用微信的人数,再补全条形统计图即可。
(3)先求出用微信的学生所占百分比,再用该校的学生人数乘以微信的学生所占百分比,计算即可得出答案。
(4)根据题意列出树状图,求出所有可能的结果数,再求出甲、乙两名同学恰好选中同一种沟通方式的可能数,然后根据概率公式求解即可。

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
| 10 | 20 | 30 |
| 60 | 55 | 50 |
(1)求y与x之间的函数关系式;

(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
【题目】小明就市电视台的各节目所受欢迎的情况,对本班50名同学进行了一次调查,结果如下:
最受学生欢迎的电视节目
节目 | 人数 |
体育 | 18 |
新闻 | 16 |
综艺 | 8 |
动画 | 5 |
其他 | 3 |
(1)选用适当的统计图描述上表数据;
(2)还能用其他统计图描述吗?