题目内容
【题目】在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20. 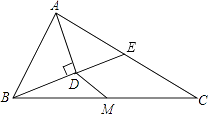
(1)求证:BD=DE;
(2)求DM的长.
【答案】
(1)证明:∵AD平分∠BAC
∴∠BAD=∠DAE
∵AD⊥BD
∴∠ADB=∠ADE=90°
在△ADB与△ADE中
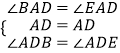
∴△ADB≌△ADE
∴BD=DE
(2)∵△ADB≌△ADE
∴AE=AB=12
∴EC=AC﹣AE=8
∵M是BC的中点,BD=DE
DM= ![]() EC=4
EC=4
【解析】(1)根据条件可证明△ADB≌△ADE,从而可得BD=DE;(2)由(1)可知:EC=AC﹣AB=8,然后根据中位线即可求出DM
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目