题目内容
【题目】阅读下列材料:
小明同学遇到下列问题:
解方程组 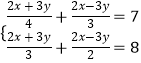 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y.
这时原方程组化为 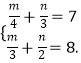 解得
解得 ![]()
把 ![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得 ![]() 解得
解得 ![]()
所以,原方程组的解为 ![]()
请你参考小明同学的做法,解决下面的问题:
(1)解方程组 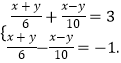
(2)若方程组 ![]() 的解是
的解是 ![]() ,求方程组
,求方程组 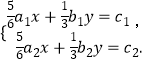 的解.
的解.
【答案】
(1)解:令m= ![]() ,n=
,n= ![]() ,
,
原方程组可化为 ![]() ,
,
解得: ![]() ,
,
∴ 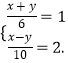 ,
,
解得 ![]()
∴原方程组的解为 ![]() ;
;
(2)解:令m= ![]() x,n=
x,n= ![]() y,
y,
原方程组可化为 ![]() ,
,
依题意,得 ![]() ,
,
∴ 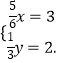 ,
,
解得 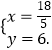 .
.
【解析】(1)令m=![]() ,n=
,n=![]() ,将方程组整理后,仿照阅读材料中的解法求出解即可;
,将方程组整理后,仿照阅读材料中的解法求出解即可;
(2)令m=![]() x,n=
x,n=![]() y,将方程组整理后,仿照阅读材料中的解法求出解即可.
y,将方程组整理后,仿照阅读材料中的解法求出解即可.
【考点精析】解答此题的关键在于理解二元一次方程组的解的相关知识,掌握二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解.

练习册系列答案
相关题目