题目内容
【题目】已知直角三角形ABC中,∠B=90°,AB=8,BC=6,BM为中线,△BMN为等腰三角形(点N在三角形AB或AC边上,且不与顶点重合),求S△BMN .
【答案】解:在直角△ABC中,AC=![]() =10,
=10,
∵BM为中线,
∴BM=CM=AM=![]() AC=5.
AC=5.
则N一定在AB上,且BM=BN=5,作MG⊥AB于点G.
∵M是AC的中点,且MG∥BC,
∴MG是△ABC的中位线,
∴MG=![]() BC=
BC=![]() ×6=3,
×6=3,
∴S△BMN=![]() BNMG=
BNMG=![]() ×5×3=
×5×3=![]() .
.
当N在AC上时,作BD⊥AC于点D.
则BD=![]() =4.8,
=4.8,
在直角△BMD中,DM=![]() =1.6,
=1.6,
则S△BMD=![]() DMBD=
DMBD=![]() ×4.8×1.6=3.84,
×4.8×1.6=3.84,
则S△BMN=2S△BMD=7.68.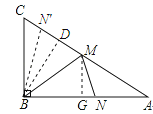
【解析】根据勾股定理求得AC的长,然后根据直角三角形斜边上的中线等于斜边的一半确定N一定在AB上,作MG⊥AB,则MG是△ABC的中位线,然后利用三角形的面积公式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.