Question

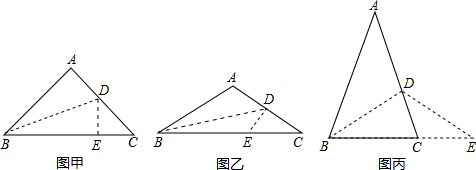
已知：在△ABC中，AB=AC，将△ABC沿BD折叠，使点A落在BC边（或延长线）上的点E处，若∠A=90°时（如图甲），易证：DE+CD+CE=BC．
当∠A＞90°时（如图乙），上述结论是否还成立？若成立，请给予证明；若不成立，请你猜想线段DE、CD、CE、BC 之间的数量关系，并证明你的猜想；
当∠A＜90°时（如图丙），线段DE、CD、CE、BC之间的又有怎样的数量关系？请写出你的猜想，不需证明．

Answer 1

分析：利用翻折变换的性质得出AD=DE，AB=BE，以及AB=BE，进而得出线段DE、CD、CE、BC 之间的数量关系即可．

解答：解：当∠A＞90°时（如图乙），上述结论DE+CD+CE=BC还成立；
理由：∵在△ABC中，AB=AC，将△ABC沿BD折叠，使点A落在BC边（或延长线）上的点E处，
∴AD=DE，AB=BE，
∵BE+EC=BC，
∴AB+EC=BC，
则AD+CD+EC=BC，
即ED+CD+EC=BC；

当∠A＜90°时（如图丙），线段DE、CD、CE、BC之间的数量关系为：DE+CD=CE+BC，
理由：∵在△ABC中，AB=AC，将△ABC沿BD折叠，使点A落在BC边（或延长线）上的点E处，
∴AD=DE，AB=BE，
∴BE=AC，
则BC+CE=AD+CD．
即DE+CD=CE+BC．

点评：本题考查了图形的翻折变换，利用折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等得出是解题关键．