题目内容
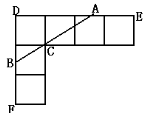
【题目】如图,正方形![]() 的边
的边![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 坐标为
坐标为![]() ,将正方形
,将正方形![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]()
![]() ,得到正方形
,得到正方形![]() ,
, ![]() 交线段
交线段![]() 于点
于点![]() ,
, ![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

(1)求证:![]() 平分
平分 ![]() ;
;
(2)在正方形![]() 绕点
绕点![]() 逆时针旋转的过程中,求线段
逆时针旋转的过程中,求线段![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(3)连结![]() 、
、![]() 、
、![]() 、
、![]() ,在旋转的过程中,四边形
,在旋转的过程中,四边形![]() 是否能在点G满足一定的条件下成为矩形?若能,试求出直线
是否能在点G满足一定的条件下成为矩形?若能,试求出直线![]() 的解析式;若不能,请说明理由.
的解析式;若不能,请说明理由.
【答案】(1)证明见解析(2)证明见解析(3)![]() .
.
【解析】试题分析:(1)根据旋转和正方形的性质可以得出CD=CB,∠CDG=∠CBG=90°,根据全等三角形的判定定理(HL)即可证出Rt△CDG≌Rt△CBG,即∠ DCG=∠BCG,由此即可得出CG平分∠DCB;
(2)由(1)的Rt△CDG≌Rt△CBG,可得出BG=DG,根据直角三角形的判定定理(HL)即可证出Rt△CHO≌Rt△CHD,即OH=HD,再根据线段间的关系即可得出![]() ;
;
(3)根据(2)的结论即可找出当G点为AB的中点时,四边形AEBD为矩形,再根据正方形的性质以及点B的坐标可得出点G的坐标,设H点的坐标为![]() ,由此可得出
,由此可得出![]() ,根据勾股定理即可求得
,根据勾股定理即可求得![]() 的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求得直线DE的解析式.
的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求得直线DE的解析式.
试题解析:(1)证明:
∵正方形![]() 绕点
绕点![]() 旋转得到正方形
旋转得到正方形![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 和
和![]() 中,
中, ![]() ,
,
∴![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
即![]() 平分
平分![]() .
.

(2)由(1)证得: ![]() ≌
≌![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中, ![]() ,
,
∴![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)四边形![]() 可为矩形..
可为矩形..
当![]() 点为
点为![]() 中点时,四边形
中点时,四边形![]() 为矩形.如图,
为矩形.如图, ![]() ,
,
由(2)证得: ![]() ,又
,又![]() ,
,
则![]() ,
,
∴四边形![]() 为矩形..
为矩形..
∵点B坐标为(6,6),
∴ AB=6,∴![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() ..
..
设![]() 点的坐标为
点的坐标为![]() ,则
,则![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,由勾股定理得:
,由勾股定理得: ![]() ,
,
解得: ![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.
设直线![]() 的解析式为:
的解析式为: ![]()
![]() ,
,
又直线![]() 过点
过点![]()
![]() 、
、![]() ,∴
,∴![]() ,解得:
,解得:  ,
,
∴ 直线![]() 的解析式为:
的解析式为: ![]() .
.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案