题目内容
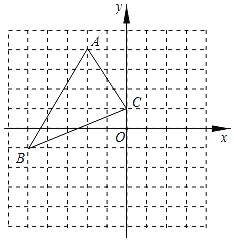
【题目】如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标(0，-1)．
（1）①作出△ABC 关于原点对称的△A1B1C1 ， 并写出点A1的坐标；
②把△ABC 绕点C逆时针旋转90°，得△A2B2C2 ， 画出△A2B2C2 ， 并写出点A2的坐标；
（2）直接写出△A2B2C2的面积
【答案】
（1）如图所示：点A 1的坐标为：（1，﹣2），点A 2的坐标为：（﹣3，﹣2）
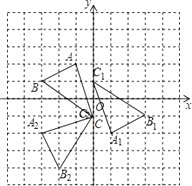
（2）解：△A 2B 2C 2的面积=3×3﹣ 
×1×3﹣ ×2×1﹣ ×3×2= 
【解析】（1）①根据关于原点对称点的坐标特点：横纵坐标都互为相反数，求出A，B，C对应点的坐标，再画图即可。
②根据旋转的性质画出旋转后的△A2B2C2，并写出点A2的坐标即可。
（2）利用面积的和差求 把三角形ABC的面积看作一个正方形的面积减去三个直角三角形的面积。
开心练习课课练与单元检测系列答案
【题目】某年级共有300名学生，为了解该年级学生在
，
两个体育项目上的达标情况，进行了抽样调査．过程如下，请补充完整．
收集数据从该年级随机抽取30名学生进行测试，测试成绩（百分制）如下：
项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74
项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75
整理、描述数据
项目的频数分布表
分组 | 划记 | 频数 |
| — | 1 |
|
| 2 |
|
| 2 |
|
| 8 |
| ||
|
| 5 |
（说明：成绩80分及以上为优秀，60～79分为基本达标，59分以下为不合格）
根据以上信息，回答下列问题：
（1）补全统计图、统计表；
（2）在此次测试中，成绩更好的项目是__________，理由是__________；
（3）假设该年级学生都参加此次测试，估计项目和项目成绩都是优秀的人数最多为________人．
