题目内容
【题目】如图,抛物线y=![]() x2﹣
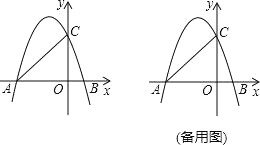
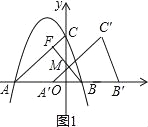
x2﹣![]() x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC,把△ABC沿x轴向右平移得到△A′B′C′,AB边上的点O平移到点O′.
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC,把△ABC沿x轴向右平移得到△A′B′C′,AB边上的点O平移到点O′.
(1)求点B、C的坐标及抛物线的对称轴;
(2)在平移的过程中,设点B关于直线A′C′的对称点为点F,当点F落在直线AC上时,求△ABC平移的距离;
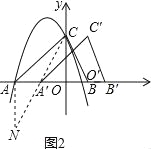
(3)在平移过程中,连接CA′,CO′,求△A′CO′周长的最小值.
【答案】(1)B(1,0),C(0,3);对称轴是直线x=﹣![]() ;
;
(2)△ABC平移的距离为![]() ;
;
(3)△A′CO′周长的最小值为4+2![]() .
.
【解析】
试题分析:(1)通过加方程![]() x2﹣
x2﹣![]() x+3=0可得A点和B点坐标,再计算自变量为0时的函数值可得到C点坐标,然后利用对称性可确定抛物线的对称轴;
x+3=0可得A点和B点坐标,再计算自变量为0时的函数值可得到C点坐标,然后利用对称性可确定抛物线的对称轴;
(2)根据轴对称的性质对称BM=FM,由平移的定义可知A′M∥AC,根据平行线分线段成比例定理即可证得AA′=BA′=![]() ,从而求得平移的距离为
,从而求得平移的距离为![]() ;
;
(3)过A点作AN⊥x轴,且AN=OC,易证得△NAA′≌△COO′,得出A′N=CO′,根据两点之间线段最短,当△A′CO′周长的最小时,A′在直线NC上,即∠AA′N=∠CA′O,即可根据AAS证得△NAA′≌△COA′,得出AA′=OA′,NA′=NA′,然后根据勾股定理求得CA′=![]() ,即可求得三角形周长的最小值.
,即可求得三角形周长的最小值.
试题解析:(1)当y=0时,![]() x2﹣
x2﹣![]() x+3=0,解得x1=1,x2=﹣4,则A(﹣4,0),B(1,0),
x+3=0,解得x1=1,x2=﹣4,则A(﹣4,0),B(1,0),
当x=0时,y=![]() x2﹣
x2﹣![]() x+3=3,则C(0,3);
x+3=3,则C(0,3);
抛物线的对称轴是直线x=![]() =﹣
=﹣![]() ;
;
(2)∵点B和点F关于直线A′C′的对称,∴BM=FM,由平移的定义可知A′M∥AC,
∴![]() =
=![]() =1,∴AA′=BA′=
=1,∴AA′=BA′=![]() AB,∵A(﹣4,0),B(1,0),∴AB=5,
AB,∵A(﹣4,0),B(1,0),∴AB=5,
∴AA′=BA′=![]() ,∴△ABC平移的距离为
,∴△ABC平移的距离为![]() ;
;
(3)过A点作AN⊥x轴,且AN=OC,
∴∠NAA′=∠COO′=90°,
在△NAA′和△COO′中,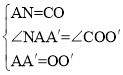
∴△NAA′≌△COO′(ASA),
∴A′N=CO′,
当△A′CO′周长的最小时,A′在直线NC上,
即∠AA′N=∠CA′O,
在△NAA′和△COA′中,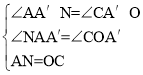
∴△NAA′≌△COA′(AAS),
∴AA′=OA′,NA′=NA′,
∴CA′=CO′,
∵OA=4,
∴AA′=OA′=2,
∴OO′=2,
∴A′O′=4,
∵OC=3,
∴CA′=![]() =
=![]() ,
,
∴△A′CO′周长的最小值为4+2![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案