题目内容

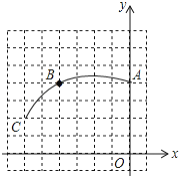
【题目】如图，已知在平面直角坐标系中，点A（0，3），点B为x轴上一动点，连接AB，线段AB绕着点B按顺时针方向旋转90°至线段CB，过点C作直线l∥y轴，在直线l上有一点D位于点C下方，满足CD＝BO，则当点B从（﹣3，0）平移到（3，0）的过程中，点D的运动路径长为_____．

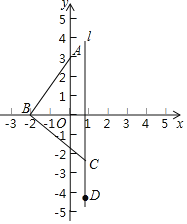
【答案】

【解析】

如图，当点B从（-3，0）平移到（3，0）的过程中，C从C1（0，-3）运动到C2（6，3），D从D1（0，-6）→D2（3，0）→D3（6，0）．求出D1D2==3，D2D3=3，即可解决问题．

如图，当点B从（﹣3，0）平移到（3，0）的过程中，C从C1（0，﹣3）运动到C2（6，3），D从D1（0，﹣6）→D2（3，0）→D3（6，0）．

D1D2＝＝3，D2D3＝3，

∴点D的运动路径长为3+3，

故答案为3+3．

练习册系列答案
相关题目

【题目】在平面直角坐标系中，直线与轴，轴分别交于点，B，与反比例函数图象的一个交点为.

（1）求反比例函数的表达式；

（2）设直线与 轴，轴分别交于点C,D,且，直接写出的值 .

【题目】如图，，是以为直径的上的点，，弦交于点．

（1）当是的切线时，求证：；

（2）已知，是半径的中点，求线段的长．

【题目】已知，如图抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB,


（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）若点E在x轴上，点P在抛物线上．是否存在以A，C，E，P为顶点且以AC为一边的平行四边形？若存在，写出点P的坐标；若不存在，请说明理由．

【题目】如图，在平面直角坐标系中，反比例函数的图象经过正方形ABCD的顶点A和B，点C、D的坐标分别是（0，﹣1）和（4，﹣3），边AD，BC分别交x轴于点E、F．

（1）填空：正方形的边长为　 　；

（2）求反比例函数y＝的解析式；

（3）若点M是直线BC上一动点，作MN∥x轴，交反比例函数y＝的图象于点N，过点M，N分别向x轴作垂线，垂足分别为P、Q，得到矩形MPQN，设点M的横坐标为a．

①填空：点N的坐标为　 　；（用含a的代数式表示）

②填空：若矩形MPQN的面积为6，则点M的横坐标为　 　．

【题目】石狮泰禾某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“十一”国庆节，商店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件．

（1）设每件童装降价x元时，每天可销售______ 件，每件盈利______ 元；（用x的代数式表示）

（2）每件童装降价多少元时，平均每天赢利1200元．

（3）要想平均每天赢利2000元，可能吗？请说明理由．

【题目】如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过格点、、，若该圆弧所在圆的圆心为点，请你利用网格图回答下列问题：

（1）圆心的坐标为_____；

（2）若扇形是一个圆锥的侧面展开图，求该圆锥底面圆的半径长（结果保留根号）．

【题目】如图，在△ABC中，AC＝BC，AB是⊙C的切线，切点为点D，直线AC交⊙C于点E、F，且CF=AC，

（1）求证：△ABF是直角三角形．

（2）若AC＝6，则直接回答BF的长是多少．

【题目】某市将开展演讲比赛活动，某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计，绘制了如下不完整的统计表和扇形统计图，

成绩等级

频数

频率

A

4

n

B

m

0.51

C

D

15

（1）求m、n的值；

（2）求“C等级”所对应的扇形圆心角的度数；

（3）已知成绩等级为A的4名学生中有1名男生和3名女生，现从中随机挑选2名学生代表学校参加全市比赛，求出恰好选中一男生和一女生的概率

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网