ЬтФПФкШн
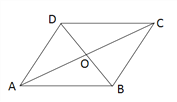
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЫФБпаЮABCDЫФЬѕБпЩЯЕФжаЕуЗжБ№ЮЊEЁЂFЁЂGЁЂHЃЌЫГДЮСЌНгEFЁЂFGЁЂGHЁЂHEЃЌЕУЕНЫФБпаЮEFGHЃЈМДЫФБпаЮABCDЕФжаЕуЫФБпаЮЃЉЃЎ
ЃЈ1ЃЉЫФБпаЮEFGHЕФаЮзДЪЧ_____ЃЌ
жЄУїФуЕФНсТлЃЎ
ЃЈ2ЃЉЕБЫФБпаЮABCDЕФЖдНЧЯпТњзу_____ЬѕМўЪБЃЌЫФБпаЮEFGHЪЧОиаЮЃЛ
ЃЈ3ЃЉЕБЫФБпаЮABCDЕФЖдНЧЯпТњзу_____ЬѕМўЪБЃЌЫФБпаЮEFGHЪЧСтаЮЃЛ
ЃЈ4ЃЉФубЇЙ§ЕФФФжжЬиЪтЫФБпаЮЕФжаЕуЫФБпаЮЪЧОиаЮЃП_____ЃЛ
ЃЈ5ЃЉФубЇЙ§ЕФФФжжЬиЪтЫФБпаЮЕФжаЕуЫФБпаЮЪЧСтаЮЃП_____ЃЛ
ЃЈ6ЃЉФубЇЙ§ЕФФФжжЬиЪтЫФБпаЮЕФжаЕуЫФБпаЮЪЧе§ЗНаЮЃП_____ЃЎ

ЁОД№АИЁП ЦНааЫФБпаЮ ACЁЭBD AC=BD СтаЮ ОиаЮ е§ЗНаЮ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСЌНгBDЃЌИљОнШ§НЧаЮЕФжаЮЛЯпЖЈРэЕУЕНEHЁЮBDЃЌEH=![]() BDЃЌFGЁЮBDЃЌFGЈT
BDЃЌFGЁЮBDЃЌFGЈT![]() BDЃЌЭЦГіЃЌEHЁЮFGЃЌEH=FGЃЌИљОнвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЕУГіЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЛ
BDЃЌЭЦГіЃЌEHЁЮFGЃЌEH=FGЃЌИљОнвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЕУГіЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉИљОнгавЛИіНЧЪЧжБНЧЕФЦНааЫФБпаЮЪЧОиаЮЃЌПЩжЊЕБЫФБпаЮABCDЕФЖдНЧЯпТњзуACЁЭBDЕФЬѕМўЪБЃЌЫФБпаЮEFGHЪЧОиаЮЃЛ
ЃЈ3ЃЉЬэМгЕФЬѕМўгІЮЊЃКAC=BDЃЌАбAC=BDзїЮЊвбжЊЬѕМўЃЌИљОнШ§НЧаЮЕФжаЮЛЯпЖЈРэПЩЕУЃЌHGЦНааЧвЕШгкACЕФвЛАыЃЌEFЦНааЧвЕШгкACЕФвЛАыЃЌИљОнЕШСПДњЛЛКЭЦНаагкЭЌвЛЬѕжБЯпЕФСНжБЯпЦНааЃЌЕУЕНHGКЭEFЦНааЧвЯрЕШЃЌЫљвдEFGHЮЊЦНааЫФБпаЮЃЌгжEHЕШгкBDЕФвЛАыЧвAC=BDЃЌЫљвдЕУЕНЫљжЄЫФБпаЮЕФСкБпEHгыHGЯрЕШЃЌЫљвдЫФБпаЮEFGHЮЊСтаЮЃЎ
ЃЈ4ЃЉСтаЮЕФжаЕуЫФБпаЮЪЧОиаЮЃЎИљОнШ§НЧаЮЕФжаЮЛЯпЦНаагкЕкШ§БпВЂЧвЕШгкЕкШ§БпЕФвЛАыПЩЕУEHЁЮBDЃЌEFЁЮACЃЌдйИљОнОиаЮЕФУПвЛИіНЧЖМЪЧжБНЧПЩЕУЁЯ1=90ЁуЃЌШЛКѓИљОнЦНааЯпЕФаджЪЧѓГіЁЯ3=90ЁуЃЌдйИљОнДЙжБЖЈвхНтД№ЃЛ
ЃЈ5ЃЉСтаЮЕФжаЕуЫФБпаЮЪЧОиаЮЃЎИљОнШ§НЧаЮЕФжаЮЛЯпЦНаагкЕкШ§БпВЂЧвЕШгкЕкШ§БпЕФвЛАыПЩЕУEHЁЮBDЃЌEFЁЮACЃЌдйИљОнОиаЮЕФУПвЛИіНЧЖМЪЧжБНЧПЩЕУЁЯ1=90ЁуЃЌШЛКѓИљОнЦНааЯпЕФаджЪЧѓГіЁЯ3=90ЁуЃЌдйИљОнДЙжБЖЈвхНтД№ЃЛ
ЃЈ6ЃЉИљОнСкБпЯрЕШЕФОиаЮЮЊе§ЗНаЮНјааНтД№ЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЫФБпаЮEFGHЕФаЮзДЪЧЦНааЫФБпаЮЃЎРэгЩШчЯТЃК
ШчЭМЃЌСЌНсBDЃЎЁпEЁЂHЗжБ№ЪЧABЁЂADжаЕуЃЌЁрEHЁЮBDЃЌEH=![]() BDЃЌЭЌРэFGЁЮBDЃЌFG=
BDЃЌЭЌРэFGЁЮBDЃЌFG=![]() BDЃЌЁрEHЁЮFGЃЌEH=FGЃЌЁрЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЛ
BDЃЌЁрEHЁЮFGЃЌEH=FGЃЌЁрЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЕБЫФБпаЮABCDЕФЖдНЧЯпТњзуЛЅЯрДЙжБЕФЬѕМўЪБЃЌЫФБпаЮEFGHЪЧОиаЮЃЎРэгЩШчЯТЃК
ШчЭМЃЌСЌНсACЁЂBDЃЎЁпEЁЂFЁЂGЁЂHЗжБ№ЮЊЫФБпаЮABCDЫФЬѕБпЩЯЕФжаЕуЃЌЁрEHЁЮBDЃЌHGЁЮACЃЎЁпACЁЭBDЃЌЁрEHЁЭHGЃЎгжЁпЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЌЁрЦНааЫФБпаЮEFGHЪЧОиаЮЃЛ
ЃЈ3ЃЉЁпEЃЌFЃЌGЃЌHЗжБ№ЪЧБпABЁЂBCЁЂCDЁЂDAЕФжаЕуЃЌЁрдкЁїADCжаЃЌHGЮЊЁїADCЕФжаЮЛЯпЃЌЫљвдHGЁЮACЧвHG=![]() ACЃЛЭЌРэEFЁЮACЧвEF=
ACЃЛЭЌРэEFЁЮACЧвEF=![]() ACЃЌЭЌРэПЩЕУEH=
ACЃЌЭЌРэПЩЕУEH=![]() BDЃЌдђHGЁЮEFЧвHG=EFЃЌЁрЫФБпаЮEFGHЮЊЦНааЫФБпаЮЃЌгжAC=BDЃЌЫљвдEF=EHЃЌЁрЫФБпаЮEFGHЮЊСтаЮЃЎ
BDЃЌдђHGЁЮEFЧвHG=EFЃЌЁрЫФБпаЮEFGHЮЊЦНааЫФБпаЮЃЌгжAC=BDЃЌЫљвдEF=EHЃЌЁрЫФБпаЮEFGHЮЊСтаЮЃЎ
ЃЈ4ЃЉСтаЮЕФжаЕуЫФБпаЮЪЧОиаЮЃЎРэгЩШчЯТЃК
ШчЭМЃЌСЌНсACЁЂBDЃЎЁпEЁЂFЁЂGЁЂHЗжБ№ЮЊЫФБпаЮABCDЫФЬѕБпЩЯЕФжаЕуЃЌspan>ЁрEHЁЮBDЃЌHGЁЮACЃЌFGЁЮBDЃЌEH=![]() BDЃЌFG=
BDЃЌFG=![]() BDЃЌЁрEHЁЮFGЃЌEH=FGЃЌЁрЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЎ
BDЃЌЁрEHЁЮFGЃЌEH=FGЃЌЁрЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁрACЁЭBDЃЎЁпEHЁЮBDЃЌHGЁЮACЃЌЁрEHЁЭHGЃЌЁрЦНааЫФБпаЮEFGHЪЧОиаЮЃЛ
ЃЈ5ЃЉОиаЮЕФжаЕуЫФБпаЮЪЧСтаЮЃЎРэгЩШчЯТЃК
РэгЩШчЯТЃК
ШчЭМЃЌСЌНгACЁЂBDЃЎдкЁїABDжаЃЌЁпAH=HDЃЌAE=EBЃЌЁрEH=![]() BDЃЌЭЌРэFG=
BDЃЌЭЌРэFG=![]() BDЃЌHG=
BDЃЌHG=![]() ACЃЌEF=
ACЃЌEF=![]() ACЃЎгжЁпдкОиаЮABCDжаЃЌAC=BDЃЌЁрEH=HG=GF=FEЃЌЁрЫФБпаЮEFGHЮЊСтаЮЃЎ
ACЃЎгжЁпдкОиаЮABCDжаЃЌAC=BDЃЌЁрEH=HG=GF=FEЃЌЁрЫФБпаЮEFGHЮЊСтаЮЃЎ
ЃЈ6ЃЉСЌНгACЁЂBDЃЎЁпEЁЂFЁЂGЁЂHЗжБ№ЪЧABЁЂBCЁЂCDЁЂDAЕФжаЕуЃЌЁрEF=![]() ACЃЌGH=
ACЃЌGH=![]() ACЃЌEH=
ACЃЌEH=![]() BDЃЌGF=
BDЃЌGF=![]() BDЃЎЁпAB=CDЃЌЁрAC=BDЃЌЁрEF=GH=EH=GFЃЌЁрЫФБпаЮEFGHСтаЮЃЎЁпЁЯHEF=90ЁуЃЌЁрЫФБпаЮEFGHе§ЗНаЮЃЎЙЪД№АИЮЊЃКЦНааЫФБпаЮЃЛACЁЭBDЃЛAC=BDЃЛСтаЮЃЛОиаЮЃЛе§ЗНаЮЃЎ
BDЃЎЁпAB=CDЃЌЁрAC=BDЃЌЁрEF=GH=EH=GFЃЌЁрЫФБпаЮEFGHСтаЮЃЎЁпЁЯHEF=90ЁуЃЌЁрЫФБпаЮEFGHе§ЗНаЮЃЎЙЪД№АИЮЊЃКЦНааЫФБпаЮЃЛACЁЭBDЃЛAC=BDЃЛСтаЮЃЛОиаЮЃЛе§ЗНаЮЃЎ


 ЧсЧЩЖсЙкжмВтдТПМжБЭЈжаПМЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈжаПМЯЕСаД№АИЁОЬтФПЁПФГЙЄГЇМЦЛЎЩњВњAЃЌBСНжжВњЦЗЙВ10МўЃЌЦфЩњВњГЩБОКЭРћШѓШчЯТБэЃК
AжжВњЦЗ | BжжВњЦЗ | |
ГЩБОЃЈЭђдЊ/МўЃЉ | 2 | 5 |
РћШѓЃЈЭђдЊ/МўЃЉ | 1 | 3 |
ЃЈ1ЃЉШєЙЄГЇМЦЛЎЛёРћ14ЭђдЊЃЌЮЪAЃЌBСНжжВњЦЗгІЗжБ№ЩњВњЖрЩйМўЃП
ЃЈ2ЃЉШєЙЄГЇМЦЛЎЭЖШызЪН№ВЛЖргк44ЭђдЊЃЌЧвЛёРћЖргк14ЭђдЊЃЌЮЪЙЄГЇгаФФМИжжЩњВњЗНАИЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌФФжжЩњВњЗНАИЛёРћзюДѓЃПВЂЧѓГізюДѓРћШѓЃЎ