Question

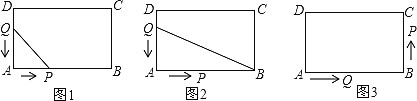
【题目】如图,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm、s的速度移动.如果P、Q同时出发,用(秒)表示移动的时间,那么:

(1)如图1,当为何值时,△QAP为等腰直角三角形?

(2)如图2,当为何值时,△QAB的面积等于长方形面积的

(3)如图3,P、Q到达B、A后继续运动,P点到达C点后都停止运动.当为何值时,线段AQ的长等于线段CP的长的一半?

Answer 1

【答案】（1）3；（2）；（3）7.5

【解析】

（1）根据已知条件得到DQ=tcm，AQ=（6-t）cm，根据三角形的面积列方程即可得到结论；

（2）根据等腰三角形的性质列方程即可得到结论；

（3）根据已知条件得到AQ=（t-6）cm，CP=（18-2t）cm，依题意使线段AQ的长等于线段CP的长的一半，列方程即可得到结论．

（1）由题可知：DQ=tcm，AQ=（6-t）cm，

∵△QAB的面积=（6-t）×12，

依题意得：（6-t）×12=×6×12，

解得：t=3；

（2）由题可知：DQ=tcm，AQ=（6-t）cm，AP=2tcm，

使△QAP为等腰三角形，

∴AQ=AP，

6-t=2t

解得t=2；

（3）由题可知：AQ=（t-6）cm，CP=（18-2t）cm，

依题意使线段AQ的长等于线段CP的长的一半，

∴t-6=（18-2t），

解得：t=7.5．