题目内容
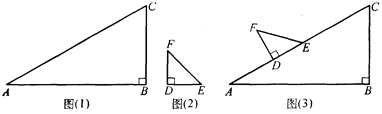
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图(1)、图(2).在图(1)中,∠B=90°,∠A=30°;图(2)中,∠D=90°,∠F=45°.图(3)是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上,移动开始时,点D与点A重合.
(1)△DEF在移动过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用外角的性质得出∠FCE+∠CFE=∠FED=45°,即可得出答案;(2)要使FC∥AB,则需∠FCE=∠A=30°,进而得出∠CFE的度数.
(1)是定值,∠FCE+∠CFE=45°.证明如下:
如图,连接FC,∵∠DEF=∠FCE+∠CFE(外角定理),
∵∠DEF=90°-45°=45°.
∴∠CFE+∠CFE=45°
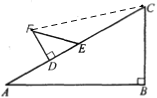
(2)能将△DEF和移动至某位置.使F、C的连线于AB平行,理由:
设CF∥AB,则∠FCE=∠A=30°,由(1)可知∠CFE=∠DEF一∠ECF
∴∠CFE=45°-30°=15°.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目