题目内容
【题目】如图,PA、PB分别切⊙O于A、B两点,点C在优弧 ![]() 上,∠P=80°,则∠C的度数为( )
上,∠P=80°,则∠C的度数为( ) 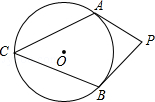
A.50°
B.60°
C.70°
D.80°
【答案】A
【解析】解:∵PA是圆的切线. ∴∠OAP=90°,
同理∠OBP=90°,
根据四边形内角和定理可得:
∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣80°=100°,
∴∠C= ![]() ∠AOB=50°.
∠AOB=50°.
故选A.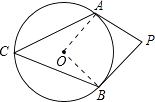
【考点精析】通过灵活运用圆周角定理和切线的性质定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

练习册系列答案
相关题目
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?