题目内容
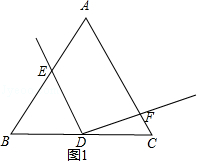
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
【答案】
(1)
解:如图1所示:
(2)
解:想法1证明:如图2,过D作DG∥AB,交AC于G,
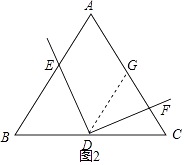
∵点D是BC边的中点,
∴DG= ![]() AB,
AB,
∴△CDG是等边三角形,
∴∠EDB+∠EDG=120°,
∵∠FDG+∠EDG=120°,
∴∠EDB=∠FDG,
∵BD=DG,∠B=∠FGD=60°,
∴△BDE≌△GDF,
∴DE=DF;
想法2证明:如图3,连接AD,
∵点D是BC边的中点,
∴AD是△ABC的对称轴,
作点E关于线段AD的对称点P,点P在边AC上,
∴△ADE≌△ADP,
∴DE=DP,∠AED=∠APD,
∵∠BAC+∠EDF=180°,
∴∠AED+∠AFD=180°,
∵∠APD+∠DPF=180°,
∴∠AFD=∠DPF,
∴DP=DF,
∴DE=DF;
想法3证明:如图4,连接AD,过D作DM⊥AB于M,DN⊥AC于N,

∵点D是BC边的中点,
∴AD平分∠BAC,
∵DM⊥AB于M,DN⊥AC于N,
∴DM=DN,
∵∠A=60°,
∴∠MDE+∠EDN=120°,
∵∠FDN+∠EDN=120°,
∴∠MDE=∠FDN,
∴Rt△MDE≌Rt△NDF,
∴DE=DF
(3)
解:当点F在AC边上时,BE+CF= ![]() AB,
AB,
当点F在AC延长线上时,BE﹣CF= ![]() AB,
AB,
证明:①当点F在AC边上时,如图5中,过点D作DM⊥AB于M,作DN⊥AC于N.

∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
在△BDM与△CDN中,  ,
,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC﹣FN=2BM=BD= ![]() AB;
AB;
②当点F在AC延长线上时,如图6,
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD= ![]() AB,
AB,
综上所述:当点F在AC边上时,BE+CF= ![]() AB;
AB;
当点F在AC延长线上时,BE﹣CF= ![]() AB.
AB.
【解析】(1)根据题目中的要求作图即可;(2)想法1,由已知得到△CDG是等边三角形,证得∠EDB=∠FDG,根据全等三角形的性质即可得到结论;想法2,如图3,连接AD,作点E关于线段AD的对称点P,点P在边AC上,根据全等三角形的性质得到DE=DP,∠AED=∠APD,等量代换得到∠AFD=∠DPF,于是得到结论;想法3,如图4,连接AD,过D作DM⊥AB于M,DN⊥AC于N,根据角平分线的性质得到DM=DN,根据全等三角形的性质即可得到结论;(3)当点F在AC边上时,过点D作DM⊥AB于M,作DN⊥AC于N.只要证明△BDM≌△CDN,△EDM≌△FDN即可解决问题,当点F在AC延长线上时,证明方法类似.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?