Question

【题目】如图，过点A（2，0）的两条直线L1、L2分别交y轴于点B、C，其中点B在原点上方，点C在原点下方，已知AB= ．
（1）求点B的坐标；
（2）若△ABC的面积为4，请求出点C的坐标，并直接写出直线L2所对应的函数关系式．

Answer 1

【答案】
（1）解：∵点A的坐标为（2，0），

∴AO=2，

在直角三角形OAB中，AO2+OB2=AB2，

即22+OB2=（ ），

∴OB=3，

∴B（0，3）；

（2）解：∵△ABC的面积为4

4= BC×OA，即4= BC×2，

∴BC=4，

∴OC=BC﹣OB=4﹣3=1，

∴C=（0，1），

设l2的解析式为y=kx+b，则 ，解得 ，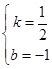

直线L2所对应的函数关系式为y= x﹣1．

【解析】（1）先根据勾股定理求得BO的长，再写出点B的坐标；（2）先根据△ABC的面积为4，求得CO的长，再根据点A、C的坐标，运用待定系数法求得直线l2的解析式．