Question

在正实数范围内，只存在一个数是关于x的方程的解，则实数k的取值范围是      .

 

Answer 1

【答案】

或或

【解析】

试题分析：先把原方程化为2x²-3x-（k+3）=0，一定是一个一元二次方程，在正实数范围内，只存在一个数是关于x的方程的解，因而可能方程有两个相同的实根，求得即可进行判断；或解方程得到的两个根中有一个是方程的增根，即x=1是方程2x²-3x-（k+3）=0的解，即可求得方程的另一解，然后进行判断；或方程有两个异号得实数根；或其中一根是0，即可求得方程的另一根，进行判断．因而这个方程中再分四种情况讨论：（1）当△=0时；（2）若x=1是方程①的根；（3）当方程①有异号实根时；（4）当方程①有一个根为0时，最后结合题意总结结果即可．

原方程可化为2x²-3x-（k+3）=0，①

（1）当△=0时，，x₁=x₂=满足条件；

（2）若x=1是方程①的根，得2×1²-3×1-（k+3）=0，k=-4；

此时方程①的另一个根为，故原方程也只有一根x=；

（3）当方程①有异号实根时，x₁x₂=＜0，得k＞-3，此时原方程也只有一个正实数根；

（4）当方程①有一个根为0时，k=-3，另一个根为x=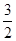，此时原方程也只有一个正实根．

综上所述，满足条件的k的取值范围是或或

考点：方程解的定义，分式的运算，根与系数的关系，根的判别式，解分式方程

点评：本题综合性强，难度较大，是中考常见题，一般出现在选择或填空的最后一题.