Question

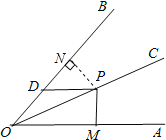
【题目】如图，OC平分∠AOB，且∠AOB＝60°，点P为OC上任意点，PM⊥OA于M，PD∥OA，交OB于D，若OM＝3，则PD的长为(　　)

A.2B.1.5C.3D.2.5

Answer 1

【答案】A

【解析】

过点P作PN⊥OB于N，根据角平分线上的点到角的两边距离相等可得PN＝PM，根据角平分线的定义求出∠AOC＝30°，然后求出PM，再根据两直线平行，同位角相等可得∠PDN＝60°，求出∠DPN＝30°，再求解即可．

如图，过点P作PN⊥OB于N，

∵OC平分∠AOB，PM⊥OA，

∴PN＝PM，

∵OC平分∠AOB，且∠AOB＝60°，

∴∠AOC＝∠AOB＝×60°＝30°，

∵OM＝3，

∴PM＝3×＝，

∵PD∥OA，

∴∠PDN＝∠AOB＝60°，

∴∠DPN＝90°﹣60°＝30°，

∴PD＝÷＝2．

故选：A．